7.Материальное уравнение эмп

Материальные уравнения

Для полного определения электромагнитного поля уравнения Максвелла необходимо дополнить материальными уравнениями, связывающими векторы и (а также и ) в веществе. В вакууме эти векторы совпадают, а в веществе связь между ними зачастую предполагают линейной:

Величины образуют тензор диэлектрической проницаемости. В принципе, он может зависеть как от точки внутри тела, так и от частоты колебаний электромагнитного поля. В изотропных средах тензор диэлектрической проницаемости сводится к скаляру, называемому также диэлектрической проницаемостью. Материальные уравнения дляприобретают простой вид

Возможны среды, для которых зависимость междуи является нелинейной (в основном — сегнетоэлектрики).

Граничные условия

На границе двух веществ скачок нормальной компоненты D_n вектора определяется поверхностной плотностью свободных зарядов:

(в СГС)

(в СИ)

Здесь  — нормальная производная,  — точка на поверхности раздела,  — вектор нормали к этой поверхности в данной точке,  — поверхностная плотность свободных зарядов. Уравнение не зависит от выбора нормали (внешней или внутренней). В частности, для диэлектриков уравнение означает, что нормальная компонента вектора непрерывна на границе сред. Простого уравнения для касательной составляющей записать нельзя, она должна определяться из граничных условий для и материальных уравнений.

8.Поляризация плоских волн

Поляризация плоских электромагнитных волн

Под поляризацией будем понимать заданную в пространстве ориентацию вектора  или . Различают 3 вида поляризации: линейную (вектор Е и Н ориентирован всегда вдоль одной линии прямой), круговую поляризация (вектор  или  вращается по кругу), эллиптическую поляризация (вектор Е или Н вращается по эллипсу).

Возьмем два ортогональных колебания:

 - показывает сдвиг во времени, они не совпадают по фазе.

Что получится в результате сложения двух ортогональных колебаний?

1) А  В амплитуды разные, а сдвиг фаз равен 0.

Сложение двух ортогональных линейно- поляризованных колебаний, изменяющихся в одной фазе, но с разной амплитудой дает линейно- поляризованное колебание ориентированное под некоторым углом.

2) 

Два ортогональных колебания по определению:

Сложение двух ортогональных линейно - поляризованных колебаний изменяющихся с одинаковой амплитудой и фазой со сдвигом  дает вращающее колебание (колебание с круговой поляризацией).

Направление вращения определяется опережением или отставанием по фазе.

3) В общем случае, когда А  В, и фазы разные, вектор  или  вращается по эллипсу.

Любую волну с линейной поляризацией можно представить в виде двух волн с круговой поляризацией, имеющих разное направление.

Явление поляризации широко используется на практике. Все приемные устройства: служебная связь - вертикальная поляризация, в России прием ТВ на горизонтальную поляризацию, вертикальная поляризация - режим передачи, горизонтальная - режим приема. Круговая поляризация широко используется в радиолокации.

9.Замедляющие структуры их типы характеристики

ЗАМЕДЛЯЮЩАЯ СИСТЕМА (замедляющая структура) - устройство, формирующее и канализирующее эл--магн. волны с фазовой скоростью v, меньшей скорости света с в вакууме (замедленные волны) и обеспечивающее их длительное, синхронное взаимодействие с потоками заряж. частиц. Величину п=с/v наз. коэф. замедления (замедлением), формально она совпадает с показателем преломления нек-рой эфф. среды. Эффект замедления достигается при помощи сплошных однородных сред с большими диэлектрич. и (или) магн. проницаемостями. Другой класс 3. с. связан с использованием неоднородных по длине (обычно периодич. или почти периодич.) структур. Это могут быть чисто металлич. устройства (спирали, волноводы с гофрир. стенками, цепочки связанных резонаторов и т. п.). Именно такие 3. с. п преобладают на практике (рис. 1).

Рис. 1. Примеры замедляющих систем: а - однозаходная спираль;б - волновод с гофрированными стенками; в - гребёнка; г - диафрагмированный волновод.

В спиральных 3. с. замедление п главной волны примерно равно отношению длины проводящих "нитей" спирали к длине их намотки, что позволяет интерпретировать механизм замедления как распространение волн тока со скоростью с вдоль этих проводящих нитей, т. е. по удлинённому пути (рис. 2). При этом дисперсия (зависимость n от w) отсутствует, групповая скорость равна фазовой.

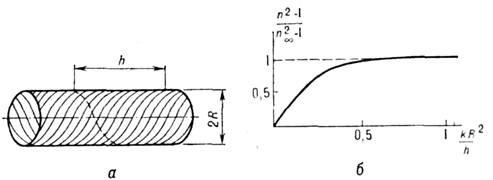РИС. 2. Модель спиральных замедляющихся систем: а - сплошной цилиндр с анизотропной проводимостью, бесконечной вдоль витков и нулевой перпендикулярно им; б - дисперсионная зависимость осесимметричной волны в нём, n_:=lim n при kR²/h'':, k=w/c.

В периодич. 3. с. любую компоненту поля нормальной волны u(r, t) = Reu₀(r)•ехр(iwt) можно представить в виде суперпозиции т, н. пространств, гармоник (ПГ) (следствие Флоке теоремы):

где z - осевая, a r₁ - поперечная к ней координаты; е_т(r_^) - амплитуда m-й ПГ, b_m=b₀+2pm/d - её волновое число, причём обычно полагают |b₀|<|b_m|; d - период 3. с. Фазовые скорости ПГ v_m=w/b_mотличаются друг от друга Эффективность взаимодействия ВЧ-поля с движущимися частицами в 3. с. характеризуется в электронных СВЧ-приборах сопротивлением связи R_св = |Е_т|²/2b²_тР, а в ускорителях - шунтовым сопротивлением R_т=|Е_т|²/2aР, где Р - поток энергии через поперечное сечение 3. с., Е_т- компонента поля синхронной гармоники, действующая на заряж. частицы, a - коэф. затухания волн. Важной особенностью нормальных волн в любой пе-риодич. системе являются частотные полосы ненропускания, когда Imb_m№0 даже в системах без потерь. Любую систему, направляющую волны, фазовая скорость к-рых меньше скорости однородной волны в окружающем свободном пространстве, можно отнести к 3. с., независимо от её назначения.