2 Основные методы интегрирования

2.1 Метод непосредственного интегрирования

Метод интегрирования, при котором данный интеграл путём тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределённого интеграла приводится к одному или нескольким табличным, называется непосредственным интегрированием

Замечание

Под тождественными преобразованиями будем понимать:

- применение формул элементарной математики;

- почленное деление числителя подынтегрального выражения на знаменатель;

- дополнительные или искусственные преобразования, которые не нарушают равносильности выражения.

2.1.10 Интегрирование алгебраических функций

Выполните самостоятельно

1

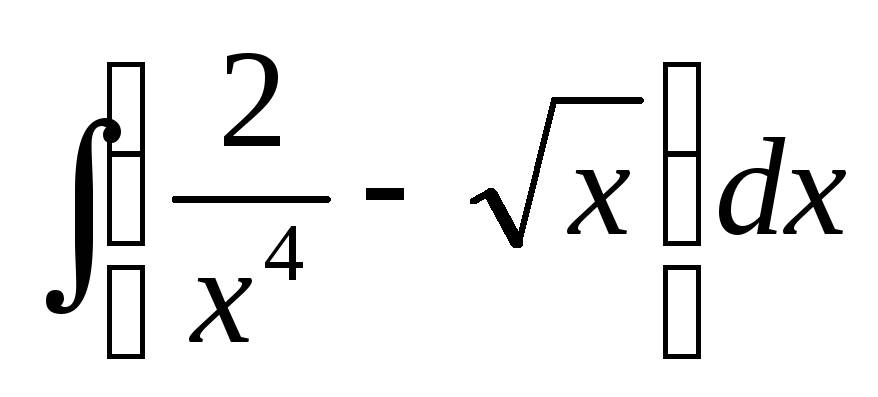
2

3

4

2.1.2

2.1.3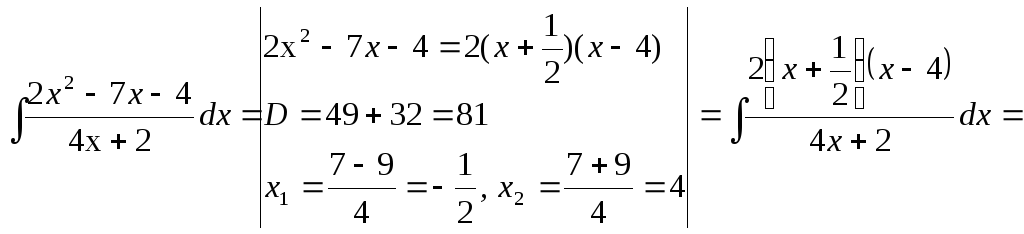

2.1.4

Выполните самостоятельно

5		6		7		8
9		10		11		12

Указания: 8 Примените формулу

9 Числитель ПФ разложите на множители:

10 В числителе ПФ примените формулу:

11 Числитель ПФ разложите на множители:

2.1.20 Интегрирование тригонометрических функций

2.1.5

2.1.6

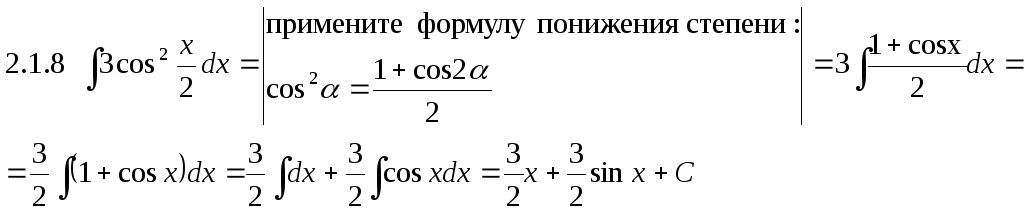
2.1.9 =|примените формулу: |= = |примените формулу |= = =| примените формулы |=

Выполните самостоятельно

13

14

15

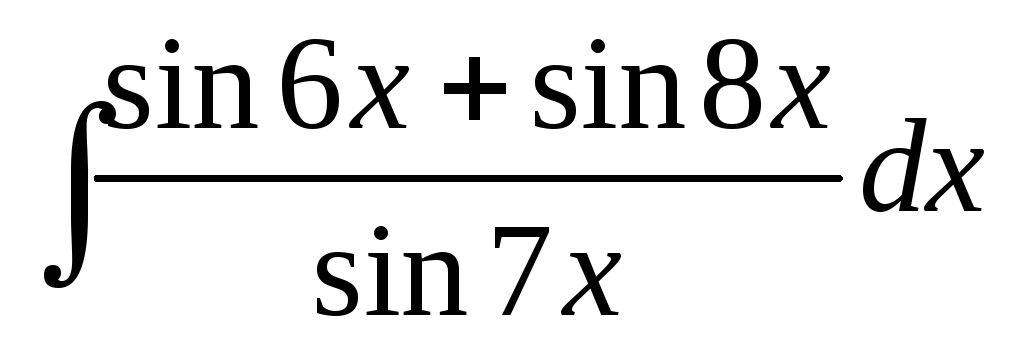
16

Указание В интегралах 13,14 примените формулу и выполните почленное деление числителя ПФ на знаменатель.

2.1.30 Интегрирование дробно- рациональных функций с помощью дополнительных преобразований

Замечание При вычислении неопределенных интегралов непосредственным способом применяются дополнительные или искусственные преобразования, не нарушающие равносильности подынтегральной функции.

Рассмотрите на конкретных примерах

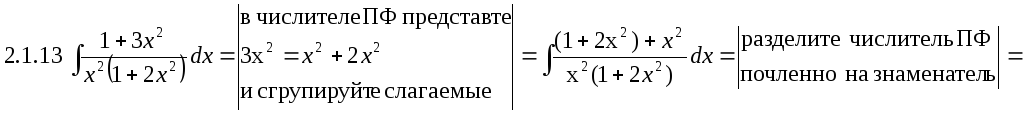
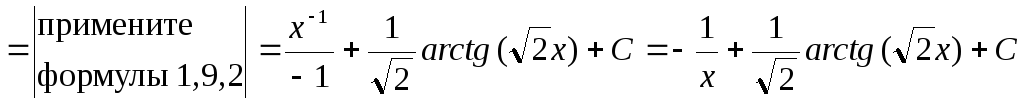
Выполните самостоятельно

17		18		19		20
21		22		23		24