СОДЕРЖАНИЕ
|
|
Пояснительная записка |
2 |
|
1 |
Неопределенный интеграл |
|
|
1.1 |
Понятие неопределенного интеграла |
|
|
1.2 |
Свойства неопределённого интеграла |
|
|
1.3 |
Таблица основных интегралов |
|
|
2 |
Основные методы интегрирования |
|
|
2.1 |
Метод непосредственного интегрирования |
|
|
2.1.10 |
Интегрирование алгебраических функций |
|
|
2.1.20 |
Интегрирование тригонометрических функций |
|
|
2.1.30 |
Интегрирование дробно- рациональных функций с помощью дополнительных преобразований |
|
|
2.2 |
Метод интегрирования подстановкой (замена переменной) |
|
|
2.2.10 |
Интегрирование функций (табличные интегралы) к аргументу, которых прибавляется постоянная величина |
|
|
2.2.20 |
Интегрирование функций (табличные интегралы) аргумент, которых умножается на постоянную величину |
|
|
2.2.30 |
Интегралы
вида:
|
|
|
2.2.40 |
Интегрирование дробных функций (рациональных или иррациональных), когда в знаменатели или под корнем в знаменатели стоит функция, производная которой равна числителю (или приводится к числителю). |
|
|
2.2.50 |
Интегралы
вида:
|
|
|
2.2.60 |
Интегрирование простейших иррациональных функций |
|
|
2.2.70 |
Интегрирование с помощью преобразования подынтегральной функции |
|
|
2.3 |
Интегрирование по частям |
|
|
|
|
|
,
Пояснительная записка
Настоящее учебно-методическое пособие состоит из двух частей:
1 Неопределенный интеграл
2 Основные способы интегрирования
2.1 Непосредственный способ интегрирования
2.2 Метод интегрирования подстановкой
2.3 Интегрирование по частям.
Каждый способ структурирован по общим признакам интегрирования, содержит набор интегралов с решениями и для самостоятельного решения студента. Интегралы для самостоятельного решения частично сопровождаются указаниями к выполнению, пронумерованы от 1 до 100.
Такая структура учебно-методического пособия делает его удобным для самостоятельного овладения основными способами интегрирования при минимальной помощи со стороны преподавателя.
В пособии представлены образцы интегрирования функций. По тексту для всех рассматриваемых интегралов предусмотрена нумерация согласно способа интегрирования.
2.1 Непосредственный способ интегрирования
-
2.1.1
2.1.2
2.1.3
2.1.4
2.1.5
2.1.6
2.1.7
2.1.8
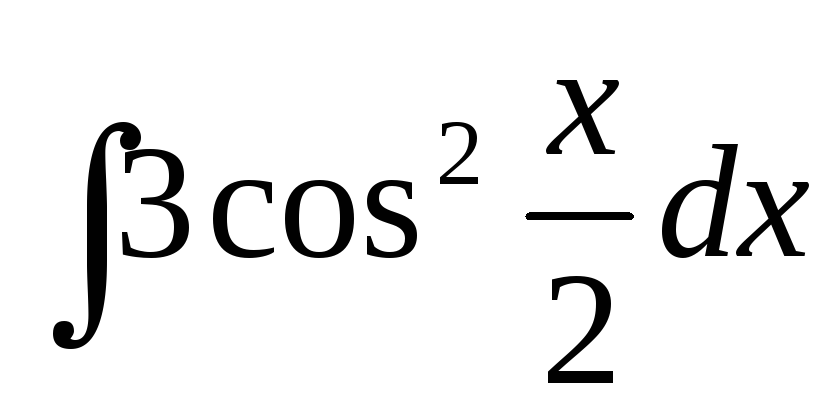
2.1.9
2.1.10
2.1.11
2.1.12
2.1.13
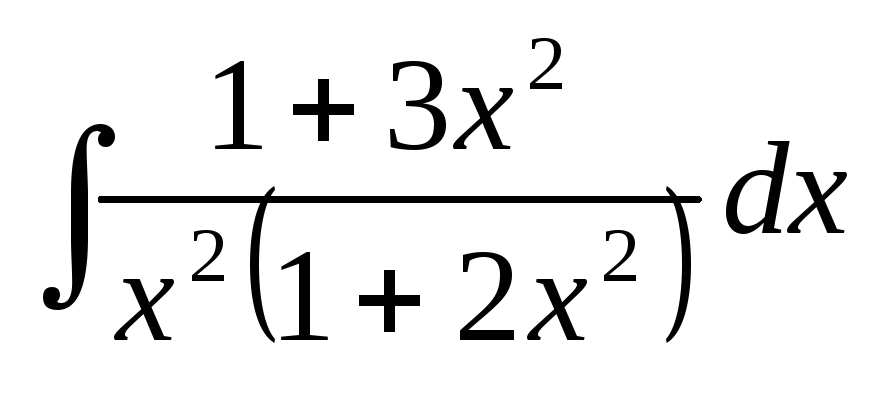
2.2 Метод интегрирования подстановкой (заменой переменной)
-
2.2.1
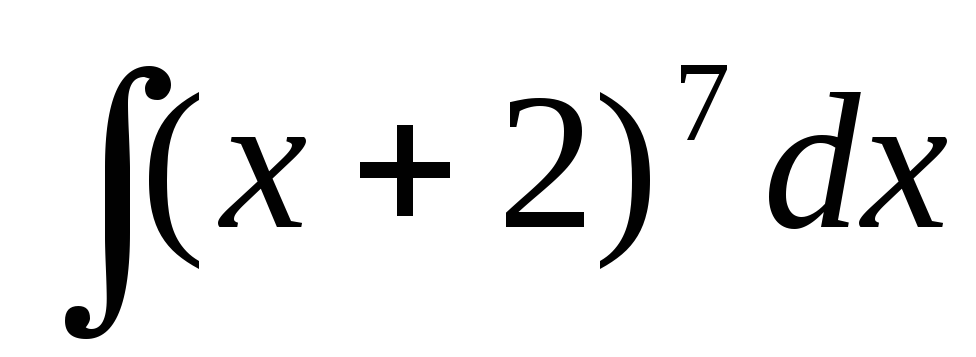
2.2.2
2.2.3
2.2.4
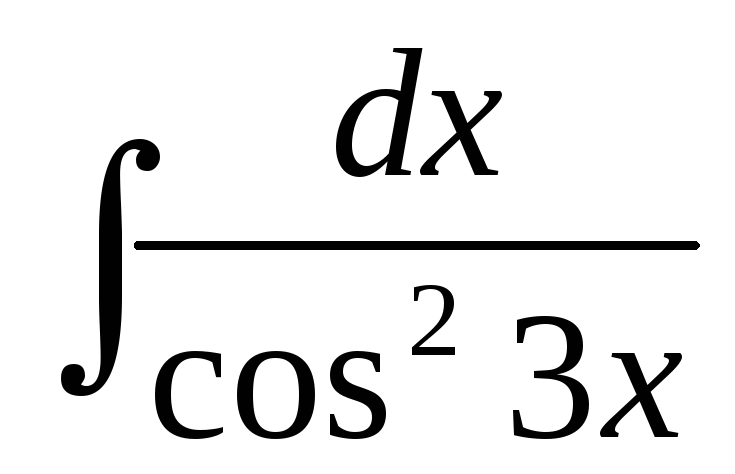
2.2.5
2.2.6
2.2.7
2.2.8
2.2.9
2.2.10
2.2.11
2.2.12
2.2.13
2.2.14
2.2.15
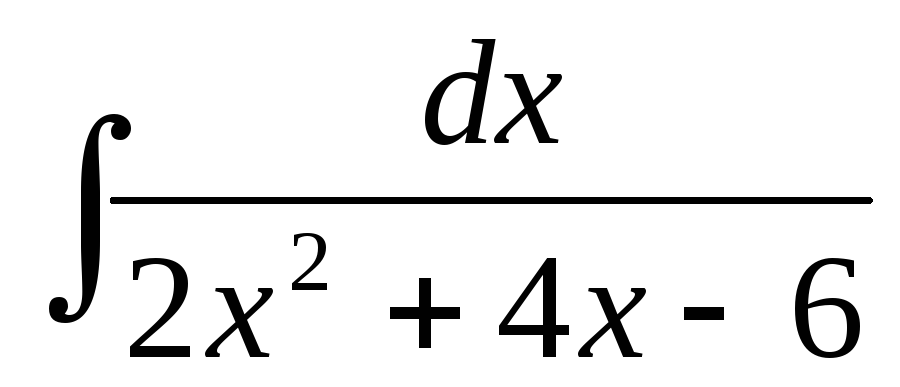
2.2.16
2.2.17
2.2.18
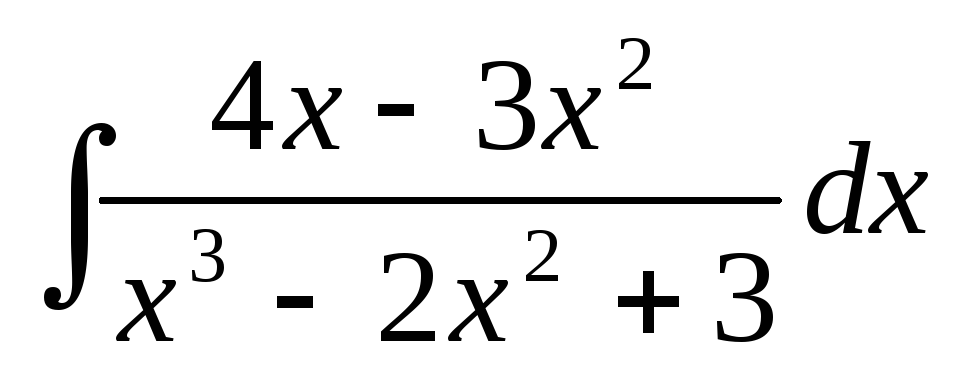
2.2.19
2.2.20
2.2.21
2.2.22
2.2.23
2.2.24
2.2.25
2.2.26
2.2.27
2.2.28
2.2.29
2.2.30
2.2.31
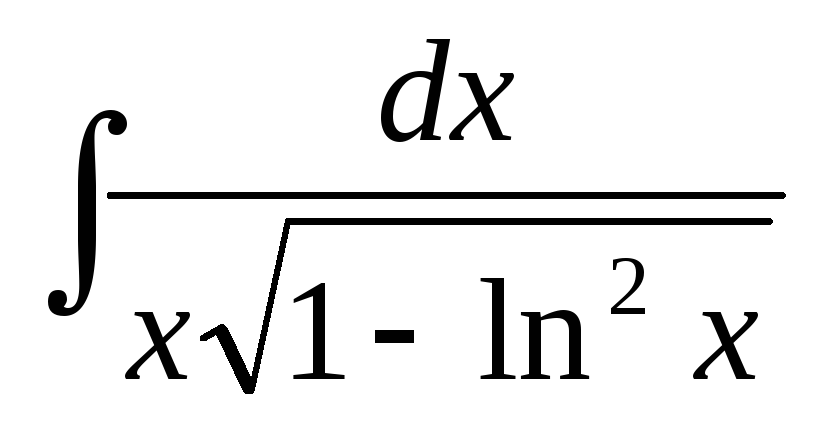
2.2.32
2.2.33
2.2.34
2.2.35
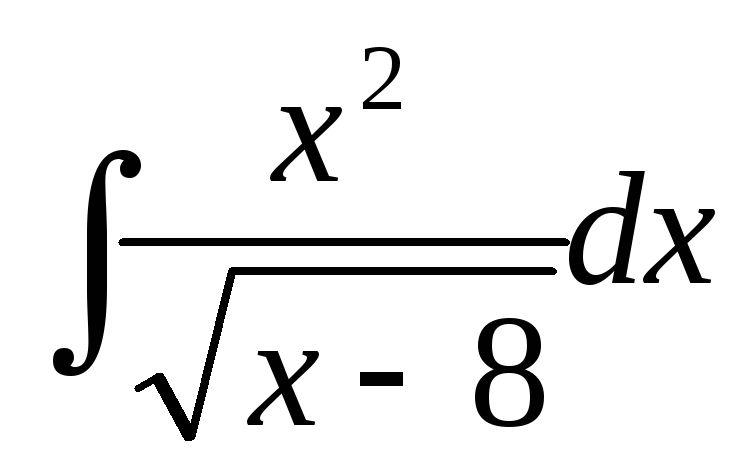
2.2.36
2.2.37
2.2.38
2.2.39
2.2.40
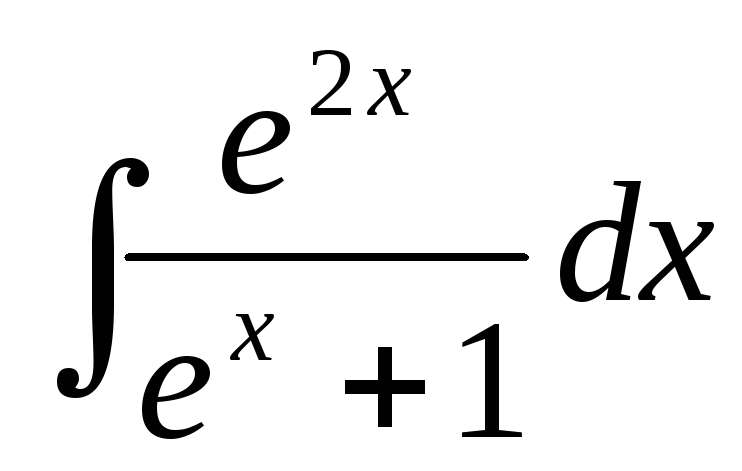
2.2.41
2.3 Метод интегрирования по частям
-
2.3 .1
2.3.2
2.3.3
2.3.4
2.3.5
2.3.6
2.3.7
2.3.8
2.3.9
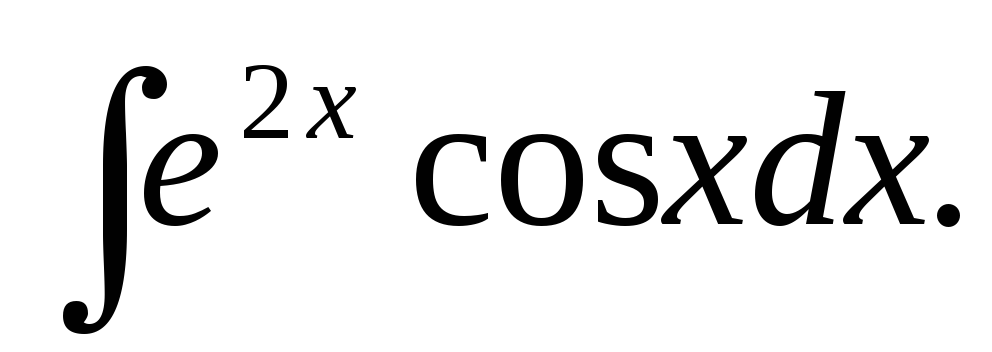
Пособие может быть использовано студентами для самостоятельного изучения соответствующего материала, выполнения практического занятия 16 Основные способы интегрирования и самостоятельной работы студента 16 Интегрирование функций: непосредственным способом, заменой переменной, по частям.
Данное учебно-методическое пособие является базовым для подготовке студентов к экзамену по модулю ЕН.01.М.07 Интегральное исчисление.
Работая с пособием, студенты имеют возможность одновременно обращаться к учебной и справочной литературе:
- Бермант, А.Ф. Краткий курс математического анализа: Учеб. Пособие/ Бермант А.Ф., Араманович И.Г. – 8-е изд., стер. – М.: Наука, 1973. – 720с.: ил.