Тема 5. Распределение признака в совокупности
Приступая к изучению темы, необходимо прежде всего составить себе представление о происхождении различия в величине количественного признака у отдельных единиц изучаемого явления в пределах однородной совокупности. Далее следует усвоить приемы построения ряда распределения при изучении вариации дискретных и непрерывно изменяющихся признаков.
Для измерения вариации (колеблемости) признака могут быть использованы следующие показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение и коэффициент вариации.
Три последних показателя обладают преимуществами, обусловленными их математическими свойствами, перед первыми двумя.
размах вариации
, (5.1)
среднее линейное отклонение
. (5.2)
Дисперсией называется средний квадрат отклонений вариантов от их средней величины. Формула расчета:
. (5.3)
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии, т.е.
. (5.4)
Этот показатель измеряет абсолютный размер колеблемости признака и выражается в тех же единицах измерения, что и значения признака.
Коэффициент вариации позволяет сравнивать колеблемость (вариацию) различных, но взаимосвязанных явлений (или их признаков), а также колеблемость одноименных признаков, но действующих в различных условиях места или времени.
Формула расчета:
. (5.5)
При рассмотрении показателя дисперсии необходимо обратить внимание на правило сложения дисперсий.
Тема 6. Ряды динамики
Задача темы – изучение методов построения статистических показателей, характеризующих изменение явлений во времени. В процессе изучения темы надо представить сущность рядов динамики и усвоить правила их построения, соблюдение которых обеспечивает сопоставимость статистических рядов динамики и позволяет осуществить их научный анализ.
В процессе анализа используются аналитические и обобщающие показатели рядов динамики: уровень ряда, абсолютный прирост, темпы роста и прироста, значение одного процента прироста, коэффициенты опережения и ускорения.
Абсолютный прирост:
-
базисный
(6.1) -
цепной
(6.2)
Темп роста:
-
базисный
(6.3) -
цепной
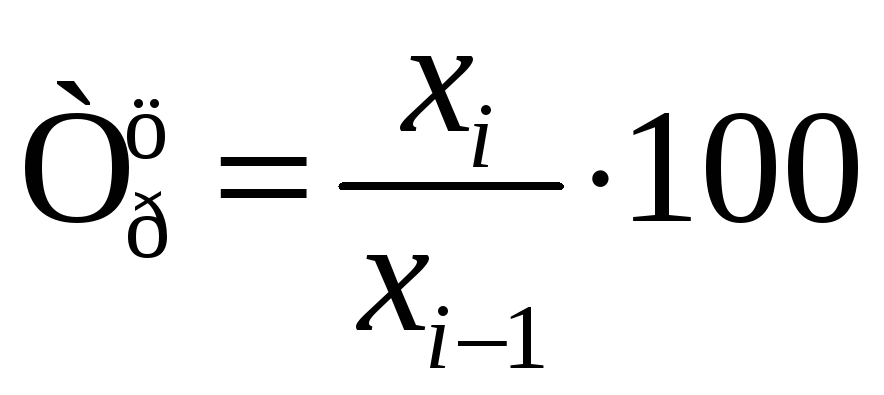(6.4)
Темп прироста:
-
базисный
(6.5) -
цепной
, (6.6)
где
– текущий уровень ряда динамики;
– предшествующий текущему уровень ряда
динамики;
– базисный (начальный) уровень ряда
динамики.
При рассмотрении приемов обработки и анализа данных ряда динамики следует использовать знание принципов взаимосвязи между показателями ряда динамики:
-
произведение ряда последовательных цепных коэффициентов роста равно соответствующему базисному коэффициенту роста;
-
частное от деления последующего базисного коэффициента роста на предыдущий равно соответствующему цепному коэффициенту;
-
темп прироста может быть рассчитан путем вычитания ста (процентов) из соответствующего значения показателя темпа роста:
; (6.7)
-
абсолютное значение 1 % прироста составляет 0,01 предшествующего уровня ряда динамики.
Для получения аналитических характеристик ряда динамики исчисляются и средние показатели.
Средний уровень периодического ряда динамики и средний абсолютный прирост определяют по формуле средней арифметической. Средний уровень моментного ряда исчисляется по формуле средней хронологической. Средний темп роста определяется по формуле средней геометрической, а средний темп прироста равняется соответствующему среднему темпу роста минус 100:
. (6.8)
Особое внимание следует уделить изучению закономерностей изменения ряда в целом: сглаживанию и выравниванию рядов динамики, интерполяции и экстраполяции.