Глава 4
Экономическая динамика со скалярными дифференциальными уравнениями
Данная глава применяет понятия и теоремы двух предыдущих глав, чтобы анализировать различные модели в экономической модели. Хотя экономические связи в этих моделях сложные, как привило, мы покажем, что динамика всех этих моделей определяется движением одномерных дифференциальных уравнений. Раздел 4.1 рассматривает односекторную модель роста. Экономический механизм этой модели будет применяться к некоторым другим моделям в этой книге, мы объясним экономическую структуру в деталях. В этом разделе также будет применяться теорема Ляпунова, чтобы гарантировать глобальную асимптотическую устойчивость равновесия. Раздел 4.2 изображает один сектор модели роста, предложенный в разделе 4.1, используя моделирование. Раздел 4.3 рассматривает односекторную модель роста для общей функции полезности. Раздел 4.4 рассматривает модель городского экономического роста жилищного строительства. В разделе 4.5 мы рассмотрим динамическую модель, чтобы увидеть как свободное время и часы работы меняются с течением времени в связи с экономическим ростом. Раздел 4.6 рассматривает динамику полового разделения труда и потребления, учитывая экономический рост. Мы проиллюстрируем увеличение трудового участия женщин как «следствие» экономического роста, а также изменение условий на рынке труда. Раздел 4.7 описывает двухблочную модель Удзавы. В разделе 4.8 мы протестируем модель Удзавы с эндогенным потребительским потреблением. Модели этой главы показывают сущность экономических принципов во многих отраслях экономики, таких, как равновесная экономика (как стационарное состояние экономической динамики), теория экономического роста, городская и гендорная экономика. Основные идеи и выводы этой главы требуют некоторые книги, чтобы объяснить, если это возможно. Это и доказывает силу теории дифференциальных уравнений.
4.1 Односекторная модель роста.(ОМР)
Мы имеем дело с экономикой одного производственного сектора. Модель, предложенная в этом разделе, называется ОМР, изначально построенной Жангом. Большинство аспектов нашей модели похожи на односекторную модель роста Солоу. Предполагается, что существует одно благо экономике в стадии рассмотрения. Домохозяйства владеют собственными активами экономики и распределяют свои доходы так, чтобы и потреблять, и сохранять. Производственные секторы или фирмы используют материалы, такие, как труд с различным уровнем человеческого капитала, различные виды капитала, знания и природные ресурсы для производства материальных благ и услуг. Обмены происходят на совершенно конкурентных рынках. Производственные секторы продают свой продукт домашним хозяйствам или в другие секторы, а домашние хозяйства продают свою рабочую силу и средства производственным секторам. Рынки факторов работают хорошо; факторы нестабильно поставляются и доступные факторы полностью используются в любой момент.
Поведение производителей
Пусть
обозначает капитал, существующий в
каждый момент времени
и
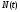- поток услуг труда в момент времени
для производства. Производственный
процесс описывается некоторой достаточно
однородной функцией
(4.4.1)
Мы
предполагаем, что
- неоклассическая (Производственная
функция называется неоклассической,
если она удовлетворяет следующим
условиям: 1 -
,
если
2 -
3
-
неотрицательны; 4 – существуют
вторые частные производные
учитывая
5 – функция однородная первой
степени,
,
6 – функция строго квазивогнута).
Мы также предполагаем, что производственная
функция показывает постоянные отдачи
от масштаба. Несложно проверить, что
линейная однородная продукция
имеет следующие свойства:
-
; -
-
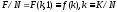и -
Теорема Эйлера имеет место
Мы изобразим
интенсивную форму
совокупной производственной функции
на Рисунке 4.1.1. Когда мы движемся вправо
вдоль производственной функции, выработка
на одного работника увеличивается в
виде капитала/труда, относительно роста
.
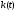Форма
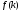на рисунке отображает предположение о
том, что имеет место падение доходности
к росту
.
Прирост выработки на одного работника
снижается по мере повышения капитала
на одного рабочего. Наклон производственной
функции становится более плоским слева
направо. Это значит, что, хотя увеличение
капитала всегда приводит к увеличению
производительности, это происходит при
снижении ставки.
Мы допускаем (идентично многочисленный) один производственный сектор. Цель его экономического производства – максимизация своей текущей прибыли
где
- цена продукции,
- процентная ставка,
- ставка заработной платы.
Мы предполагаем, что производственное благо служит хорошим средством обмена и берется в качестве масштаба цен. Таки образом, определяем
и измеряем
заработную плату и аренду потоков в
единицах произведенного блага.
Максимизация
относительно
и
в качестве переменных решений дает
(4.1.2)
Так как производственная функция является однородной первой степени, мы имеем
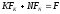
или
.
Этот означает, что общий доход используется
для оплаты всех факторов производства.
Таким образом, мы заключаем, что если
производственная функция является
однородной первой степени, то высшее
требование выполнено. (adding-up
requirement)