Степень с натуральным и рациональным показателем. Арифметический корень

С

тепенью с натуральным показателем n числа а называется произведение n сомножителей равных этому числу. - всего n сомножителей. Например, .

Число а называют основанием, а число n называют показателем степени. Степень с показателем 2 называют квадратом, а с показателем 3 – кубом. Примеры: Корнем n-ой степени (n-натуральное число) из числа a ( обозначение ) называют такое число x, степень которого равна a ().  Эту операцию называют извлечением корня n-ой степени из a. Корень из положительного числа – всегда число положительное. Корень второй степени не пишут, то есть . Например, , а не -2, хотя . Если число n – четное, то операция извлечения корня из отрицательного числа в поле действительных чисел не определена. Например, действительного числа не существует. Степенью с рациональным показателем m/n числа x (степенью с дробным показателем) называют число , m и n – целые числа.  Например, Любое число, кроме 0, в нулевой степени равно 1 . Операция не определена. Еще одно важное соотношение . Например:

Уравнения. Алгебраические уравнения

 

В алгебре рассматриваются два вида равенств - тождества и уравнения. Тождество - это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв. Для записи тождества наряду со знаком = также используется знак ≡ . Уравнение - это равенство, которое выполняется лишь при некоторых значениях входящих в него букв. Буквы, входящие в уравнение, по условию задачи могут быть неравноправны: одни могут принимать все свои допустимые значения (их называют коэффициентами, а реже параметрами, уравнения и обычно обозначав первыми буквами латинского алфавита: a,b,c,... - или теми же буквами, снабженными индексами: a1,a2,... или b1,b2,...); другие, значения которых требуется отыскать, называют неизвестными (их обычно обозначают последними буквами латинского алфавита: x,y,z,... или теми же буквами, снабженными индексами, например, x1,x2,... В общем виде уравнение с n неизвестными x1,x2,...,xn может быть записано как

F(x1,x2,...,xn)=0,

где F - некоторая функция указанных аргументов.

В зависимости от числа неизвестных уравнение называют уравнением с одним, двумя и т. д. неизвестными. Областью {множеством) допустимых значений неизвестных уравнения называют область определения функции F(x1,x2,...,xn). Значения неизвестных, обращающие уравнение в тождество, называют решениями уравнения. Уравнение считается решенным, если найдены все его решения или показано, что уравнение решений не имеет. Если все решения уравнения F=0 являются решениями уравнения G=0, то говорят, что уравнение G=0 есть следствие уравнения F=0, и пишут

F=0⇒G=0 

Два уравнения F=0 и G=0 называют эквивалентными, если каждое из них является следствием другого, и пишут

F=0⇔G=0 

Таким образом, два уравнения считаются эквивалентными, если множества решений этих уравнений совпадают.

Уравнение F=0 считают эквивалентным двум (или нескольким) уравнениям F1=0,F2=0, если множество решений уравнения F=0 совпадает с объединением множеств решений уравнений F1=0,F2=0. Некоторые эквивалентные уравнения: 1) Уравнение F+G=G эквивалентно уравнению F=0, рассматриваемому на множестве допустимых значений исходного уравнения. 2) Уравнение FG=0 эквивалентно уравнению F=0, рассматриваемому на множестве допустимых значений исходного уравнения. 3) Уравнение F·G=0 эквивалентно двум уравнениям F=0 и G=0. 4) Уравнение Fn=0 эквивалентно уравнению F=0. 5) Уравнение Fn=Gn при нечетном n эквивалентно уравнению F=G, а при четном n эквивалентно двум уравнениям F=G и F=−G .

Алгебраическим уравнением называется уравнение вида

Pn=0,

где Pn --- многочлен n-й степени от одной или нескольких переменных. Алгебраическим уравнением с одним неизвестным называется уравнение, сводящееся к уравнению вида

a0xn+a1xn−1+a2xn−2+...+an−1x+an=0,

где n - неотрицательное целое число; коэффициенты многочлена a0,a1,a2,...,an−1,an называются коэффициентами (или параметрами) уравнения и считаются заданными; x называется неизвестным и является искомым. Число n называется степенью уравнения. Значения неизвестного x, обращающие алгебраическое уравнение в тождество, называются корнями (реже решениями) алгебраического уравнения.

Арифметическая и геометрическая прогрессии

Напомним основные понятия и формулы.

Определение. Арифметической прогрессией называется последовательность чисел , ,каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d, т.е.

. (1)

Число d называется разностью арифметической прогрессии, число - первым членом, а - n-ым членом ( или общим членом ).

При любом n2 имеем:

, , (2)

поэтому для n2 имеем:

(3)

т.е., каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.

Для арифметической прогрессии с первым членом и разностью ее n-ый член можно найти по формуле

, nN. (4)

Также имеет место формула

, 1, k,n (5)

Т.е., любой член арифметической прогрессии , начиная со второго, равен полусумме равноотстоящих от него членов прогрессии.

Кроме того, справедливо равенство:

, если m+n = k+l. (6)

Сумма первых n членов арифметической прогрессии вычисляется по формуле:

(7)

Определение. Геометрической прогрессией называется последовательность чисел , nN, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же постоянное для этой последовательности число q0, т. е., . (8)

Число q называется знаменателем геометрической прогрессии, число - ее первым членом, а - n-ым ( или общим) членом.

Для геометрической прогрессии имеем:

, поэтому

(9)

Кроме того, для любых натуральных k,l,m,n имеют место формулы:

, если m+n = k+l. (10)

, если 1 (11)

т.е., квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению равноотстоящих от него членов прогрессии.

Сумма n членов геометрической прогрессии вычисляется по формуле:

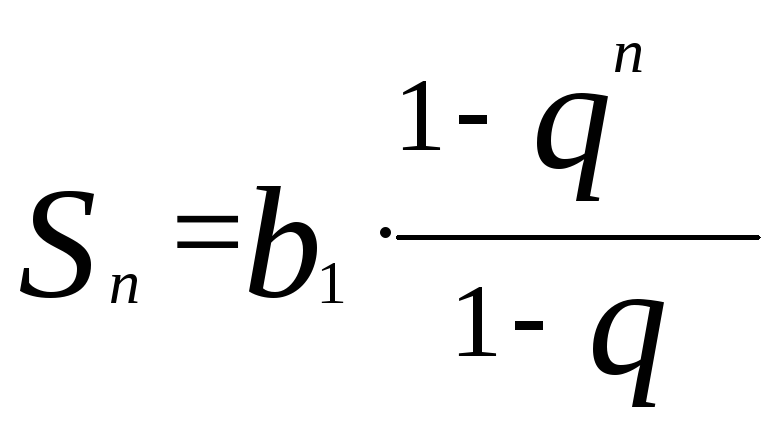(12)

Определение. Геометрическая прогрессия называется бесконечно убывающей, если ее знаменатель q подчиняется условию .

В этом случае сумма бесконечно убывающей геометрической прогрессии вычисляется по формуле: .

Пример 1. В арифметической прогрессии найти , если , а .

Решение: Т.к. , и , то запишем данные задачи в виде системы уравнений:

Решая эту систему, найдем ,. Поэтому

.

Ответ: .

Пример 2. Могут ли числа 10,25 и 40 в указанном порядке быть членами арифметической прогрессии?

Решение. Т.к. в условии не сказано, что эти числа – последовательные члены прогрессии, то будем считиать, что , где 1<m<n. Для этой пргрессии имеем систему уравнений:

,

где - разность пргрессии. Исключая из этой системы , получим следующее соотношение, связывающее натуратьные числа m и n:

.

Полагая, например, m=2, получим, что n=3, d=15 , т.е., числа m и n–натуральные и могут являться номерами членов арифметической прогресии.

Ответ. Числа 10, 25 и 40 могут быть членами арифметической прогрессии.

Пример 3. Найти количество всех трехзначных натуральных чисел, делящихся на 7 без остатка.

Решение. Наименьшим трехзначным числом, делящимся без остатка на 7, является число 105, наибольшим – число 994. Все трехзначные числа, делящиеся без остатка на 7, образуют арифметическую прогрессию с , d = 7, . Найдем n по формуле общего члена: 994= 105 + 7( n-1) , отсюда n = 128.

Ответ: Всего имеется 128 трехзначных натуральных чисел, делящихся без остатка на 7.

Пример 4. Сумма первых трех членов геометрической прогрессии равна 91. Если к этим членам прибавить, соответственно, 25, 27 и 1, то получатся три числа, образующих арифметическую прогрессию. Найти седьмой член данной геометрической прогрессии.

Решение: По условию имеем три последовательных члена геометрической прогрессии: , . Составим первые три члена арифметической прогрессии: ,, . Составим систему уравнений:

или, ,

. Разделим одно уравнение системы на другое, затем перемножим крайние с средние члены пропорции, приведем подобные члены и получим следующее уравнение :

Решим это уравнение и получим, что . Подставим эти значения в систему уравнений и найдем или .

Найдем или .

Ответ. или .