6. Использование ряда Фурье для анализа спектров периодических негармонических сигналов на примере периодической последовательности прямоугольных импульсов. Ряд Фурье

Периодический сигнал любой формы с периодом Т может быть представлен в виде суммы

гармонических колебаний с разными амплитудами и начальными фазами, частоты которых кратны основной частоте . Гармонику этой частоты называют основной или первой, остальные – высшими гармониками.

Тригонометрическая форма ряда Фурье:

,

где - постоянная составляющая;

- амплитуды косинусоидальных составляющих;

- амплитуды синусоидальных составляющих.

Четный сигнал () имеет только косинусоидальные, а нечетный ( - только синусоидальные слагаемые.

Более удобной является эквивалентная тригонометрическая форма ряда Фурье:

,

где - постоянная составляющая;

- амплитуда n-ой гармоники сигнала. Совокупность амплитуд гармонических составляющих носит название спектра амплитуд;

- начальная фаза n-ой гармоники сигнала. Совокупность фаз гармонических составляющих носит название спектра фаз.

7. Спектр периодической последовательности прямоугольных импульсов. Зависимость спектра от периода следования импульсов и их длительности. Ширина спектра. Разложение в ряд Фурье пппи

Рассчитаем амплитудный и фазовый спектры ПППИ, имеющих амплитуду , длительность , период следования и расположенных симметрично относительно начала координат (сигнал – четная функция).

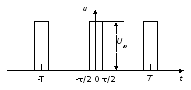
Рисунок 5.1 – Временная диаграмма ПППИ.

Сигнал на интервале одного периода можно записать:

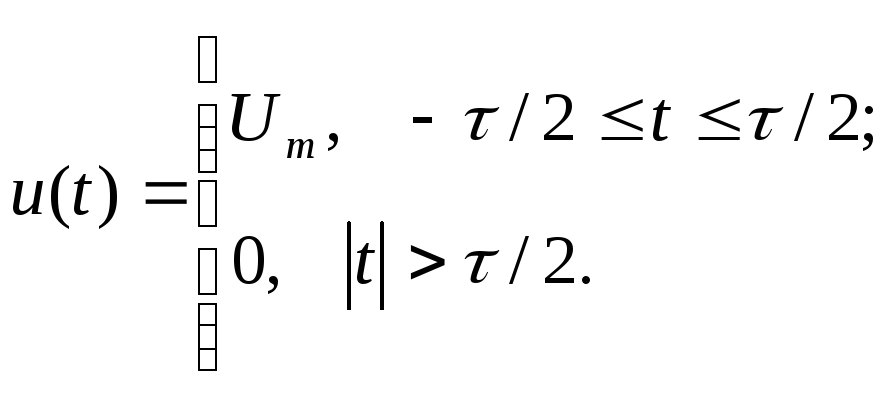
Вычисления:

,

,

,

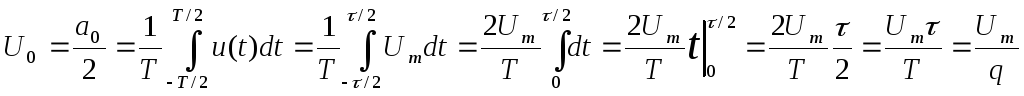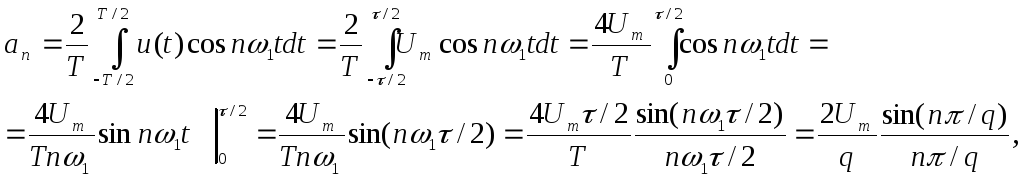
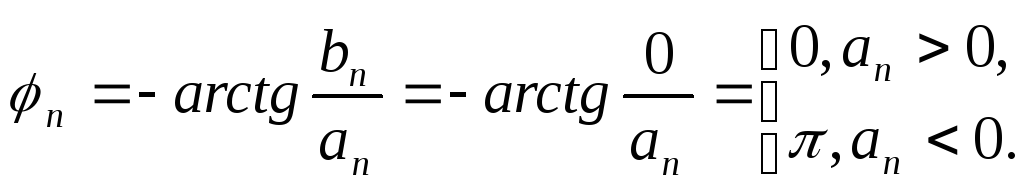
Ряд Фурье для ПППИ имеет вид:.

Рисунок 5.2 – Амплитудная спектральная диаграмма ПППИ.

Рисунок 5.3 – Фазовая спектральная диаграмма ПППИ.

Выводы:

- спектр ПППИ линейчатый (дискретный) (представляется набором отдельных спектральных линий), гармонический (спектральные линии находятся на одинаковом расстоянии друг от друга ω₁), убывающий (амплитуды гармоник убывают с ростом их номера), имеет лепестковую структуру (ширина каждого лепестка равна 2π/τ), неограниченный (интервал частот, в котором располагаются спектральные линии, бесконечен);

- при целочисленных скважностях частотные составляющие с частотами, кратными скважности в спектре отсутствуют (их частоты совпадают с нулями огибающей спектра амплитуд);

- с увеличением скважности амплитуды всех гармонических составляющих уменьшаются. При этом если оно связано с увеличением периода повторения Т, то спектр становится плотнее (ω₁ уменьшается), с уменьшением длительности импульса τ – становится больше ширина каждого лепестка;

- за ширину спектра ПППИ принят интервал частот, содержащий 95% энергии сигнала, (равен ширине двух первых лепестков огибающей):

или ;

- все гармоники, находящиеся в одном лепестке огибающей, имеют одинаковые фазы, равные либо 0 либо π.

8. Использование преобразования Фурье для анализа спектра непериодических сигналов. Спектр одиночного прямоугольного импульса. Интегральные преобразования Фурье

Сигналы связи всегда ограничены во времени и поэтому не являются периодическими. Среди непериодических сигналов наибольший интерес представляют одиночные импульсы (ОИ). ОИ можно рассматривать как предельный случай периодической последовательности импульсов (ППИ) длительностью при бесконечно большом периоде их повторения .

Рисунок 6.1 – ППИ и ОИ.

Непериодический сигнал может быть представлен суммой бесконечно большого числа бесконечно близких по частоте колебаний с исчезающе малыми амплитудами. Спектр ОИ является непрерывным и вводится интегралами Фурье:

- (1) - прямое преобразование Фурье. Позволяет аналитически отыскать спектральную функцию по заданной форме сигнала;

- (2) - обратное преобразование Фурье. Позволяет аналитически отыскать форму по заданной спектральной функции сигнала.

Комплексная форма интегрального преобразования Фурье (2) дает двустороннее спектральное представление (имеющее отрицательные частоты) непериодического сигнала в виде суммы гармонических колебаний с бесконечно малыми комплексными амплитудами , частоты которых непрерывно заполняют всю ось частот.

- комплексная спектральная плотность сигнала – комплексная функция частоты, одновременно несущая информацию как об амплитуде, так и о фазе элементарных гармоник.

Модуль спектральной плотности называется спектральной плотностью амплитуд. Его можно рассматривать как АЧХ сплошного спектра непериодического сигнала.

Аргумент спектральной плотности называется спектральной плотностью фаз. Его можно рассматривать как ФЧХ сплошного спектра непериодического сигнала.

Преобразуем формулу (2):

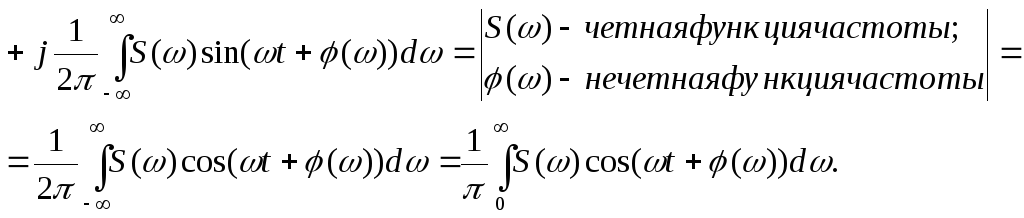
Тригонометрическая форма интегрального преобразования Фурье дает одностороннее спектральное представление (не имеющее отрицательных частот) непериодического сигнала:

.