Амплитудная модуляция

Амплитудная модуляция (АМ) – это процесс управления амплитудой гармонического несущего колебания по закону изменения информационного сигнала.

Несущее колебание описывается выражением:

,

где - амплитуда;

- полная фаза;

- угловая частота;

- начальная фаза.

При АМ амплитуда несущего колебания изменяется пропорционально мгновенным значениям модулирующего сигнала :

,

где - приращение амплитуды несущей при АМ;

- безразмерный коэффициент пропорциональности. Зависит от конкретной схемы модулятора. Выбирается так, чтобы амплитуда всегда была положительной: .

Математическая модель АМ сигнала:

.

В качестве модулирующего сигнала рассмотрим гармоническое колебание:

,

где - амплитуда модулирующего сигнала;

- его угловая частота;

- его начальная фаза.

Так как амплитуда несущей изменяется по закону модулирующего сигнала, то можно записать:

.

Запишем выражение, являющееся математической моделью АМ сигнала в случае использования в качестве информационного сигнала гармонического колебания:

где - коэффициент модуляции, причем . Коэффициент модуляции (глубина модуляции) – это отношение максимального приращения амплитуды модулированного сигнала к амплитуде несущей.

17. Сигнал с аналоговой двухполосной амплитудной модуляцией с большим уровнем несущей. Математическая модель. Спектр сигнала при модуляции гармоническим и сложным сигналами. Спектр ам сигнала

АМ сигнал можно представить в виде суммы гармонических составляющих. Используя формулу произведения косинусов:

, -

из выражения сигнала с гармонической АМ получаем:

.

АМ сигнал при модуляции гармоническим сигналом состоит из трех спектральных составляющих с частотами: несущей , нижней боковой , верхней боковой . Спеткральная диаграмма однотонального АМ сигнала симметрична относительно несущей частоты. Амплитуды боковых колебаний одинаковы () и при не превышают половины амплитуды несущего колебания.

В большинстве случаев модулирующие сигналы являются сложными. Любой сложный сигнал можно представить в виде суммы (конечной или бесконечной) гармонических составляющих, воспользовавшись рядом или интегралом Фурье. Каждая гармоническая состав­ляющая модулирующего сигнала с частотой приведет к появлению в AM сигнале двух боковых составляющих с частотами , . Т.е. в спектре сложномодулированного AM сигнала помимо колебания с частотой несущей содержатся группы верхних и нижних боковых колебаний, образующих соот­ветственно верхнюю и нижнюю боковые полосы частот. При этом верхняя боковая полоса частот является масштабной копией спектра модулирующего сигнала, сдвинутой в область высоких частот на величину . Нижняя боковая полоса частот также повторяет спектральную диаграмму сигнала , но частоты в ней располагаются в зеркальном (обратном) поряд­ке относительно несущей частоты.

Ширина спектра AM сигнала равна удвоенному значению наиболее высокой час­тоты спектра модулирующего сигнала:

.

На принципах АМ построено большинство радиовещательных систем, а также видеоканалов в телевидении.

18. Амплитудно-модулированные сигналы с подавленной несущей. Балансная (БМ) и однополосная (ОМ) модуляция. Спектры БМ и ОМ сигналов при модуляции гармоническим и сложным сигналами.

    Балансная и однополосная модуляции

Для более эффективного использования мощности спектра AM сигнала возможно исключение из спектра AM сигнала несущего колебания. Такой АМ сигнал называют балансно-модулированным (БМ). Также из спектра можно исключить одну боковую полосу час­тот (верхнюю или нижнюю), поскольку каждая из них содержит полную информацию о модулирующем сигнале . При этом получается однополосную модуляцию (ОМ), т.е. модуляцию с одной боковой полосой — ОБП.

Балансная модуляция

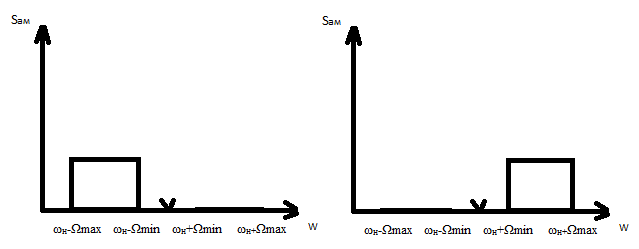
Однополосная модуляция