
Физика 3 семестр / новая папка / физика_шпоры
.doc|
1) Эл заряд – скал. физ величина, определ инт-сть эл взаимодействий. Не зависит от скор движ заряж тела. Эл заряд дискретен, т.е. сущ миним величина эл заряда (элементарный заряд), а эл заряд любого тела может быть представлен как алгебр сумма целого числа элементарн зарядов. Элем положит заряд – это заряд протона, элем отриц заряд – это заряд электрона 1 кулон – это эл заряд, переносим через поперечн сеч проводника за 1 с при силе тока в проводнике, 1 ампер.
Сист тел или частиц наз электрич изолир-ной, если между ней и внешн телами нет обмена эл зарядами. Для эл изол-ной сист тел справедлив з-н сохр эл заряда: алгебр сумма эл зарядов частиц, образ эл изолир сист, не изменяется при любых процессах, происх в этой сист. Эл-ски заряж мат точ-точечным эл заряд. З-н Кулона -сила электростатич взаимодейст двух неподвижн точ эл зарядов, нах-ся в вакууме, прямо пропорц произведен этих зарядов, обратно пропорц квадрату расст между зарядами и направл вдоль соедин их прямой
где
|
2) Электрич поле, созд-ое заряж телами, неподвижн относит инерц сист отсчета, наз электростатическим полем.
Напряж
эл поля равна
отнош силы, действ со стороны поля на
неподвижн пробный эл заряд, помещ в
рассматрив точку поля, к этому заряду:
эл
поле однородное,
если во всех его точках векторы напряж
Сила, действ со стор эл поля на помещ в него произв точ заряд, равна
Элементарн
сила со стор поля, действ на каждый
точ заряд
Линейн
плотн
эл зарядов
Поверхностн
плотн
эл зарядов
Объемн
плотн
эл зарядов
результир
сила
принцип суперпозиц элх полей (принцип независ действ электрических полей): напряж-ть эл поля, созданного систем зарядов в люб точке простр-ва, равна вект сумме напряж-ти полей, созданных кажд зарядом в отдельности в этой точке.
|
4)
Эл
поле точ заряда явл центр-ым, а поэтому
потенциальным Определ работу поля,
созд-го зарядом
Если заряды одноим, то поле соверш положит раб при их удален друг от друга и отриц при их сближ.
Работа
сил электростатич поля по перемещ
заряда не завис от формы траектор движ
заряда, а определ положен нач и конеч
точек траект. Кулоновские силы
потенциальны.
Пр
1.
Определим потенциал произв точки
простр-ва, удаленной на расст r
от точ заряда Q
выберем точку, где
Пр
2.
Рассм электрост поле, созд-ое сист
точеч зарядов
|
|
|
|
|
|
10)
Электроемкостью
уединенного проводника
наз физ величина, равная отнош заряда
проводника к его потенциалу в поле
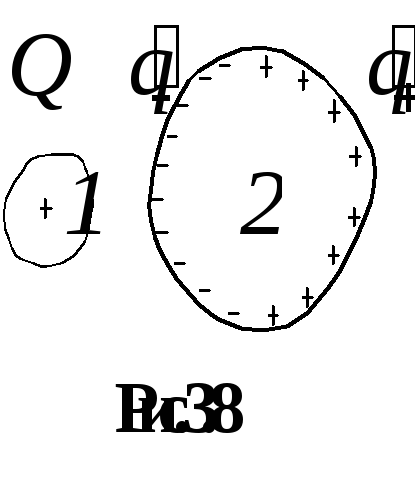
этого заряда: Электр-ть проводника показ, какой заряд необх сообщ проводн для того, чтобы его потенциал принял заданное значение. Электр-ть не завис ни от величины заряда проводника, ни от значен его потенц, а завис только от размера и формы проводника, а также от диэлектр св-в среды, в кот он нах-ся..
При опред емкости
провод опис выше спос важно, чтобы
вблизи него не нах другие провод, т.е.
чтобы был уединенным. Рассм, как измен
емкость провод, если он будет нах рядом
с незаряж провод. Допустим, что провод
1
обладает положит зар (рис. 3.8). Тогда в
незаряж проводнике 2
произойдет разделение зарядов
(элек-ская индукция) на отриц
Заметим, что
В случ, если заряж
проводн располаг т о, что эл поле сущ
только в пр-ве между ними, то они образ
конденсатор.
Сами проводн при этом наз обкладками
конденс.. Плоск конденс созд сист двух
бесконеч больш паралл пластин площ
S,
нах на малом расст d
друг от друга (
Электроемкостью
конденсатора
наз физ велич, равная отнош зар конденс
к разности потенц, создаваем полем
этого заряда между его обкладками: Так же, как и емкость проводника, электроемк конд не зав ни от велич зар конден, ни от разн потенц между его обклад, а зав только от размера и формы конден, а также от диэлектрич св-в среды между обклад конден. не завис от налич вблизи него др проводящ или диэлектр тел. Опред
алгеб сумму зар, охв поверхн гауссова
цил.
|
11)
Рассм процесс
зарядки уединен проводника. Чтобы его
заряд достиг велич Q,
будем сообщ проводн заряд порциями
dq,
перенося их из бесконечно удален точки
1
на пов-ть проводн в точку 2
Для передачи проводн нов порции заряда
Согл з-ну сохр эн, раб внеш сил по зарядке проводн увелич энер создав электр поля, т.е. проводн запасает определенную энергию:
где Q
– заряд конденс после зарядки. Тогда
энерг эл поля, создан конденс
Преобраз
последн равен для случ плоск конденс:
где
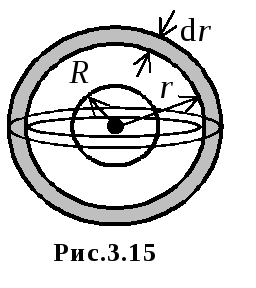
Объемной
плотностью энергии поля
называется отношение энергии поля,
заключ в малом объеме простр к этому
объему:
случай
неоднородн поля:
Поскол
напряж поля завис только от радиальн
коорд, то она будет практич постоянна
в пределах тонк сферич слоя с внутр
рад r
и толщ
|
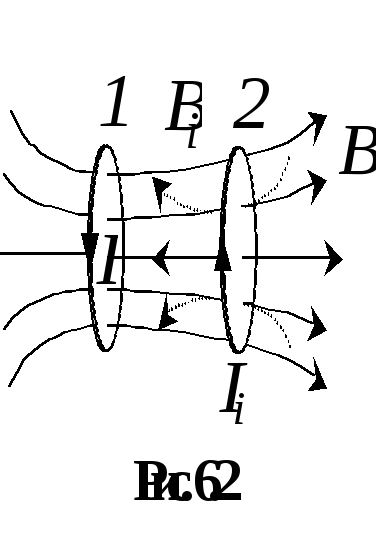
Разместим на одном сердечнике две проводящие катушки (рис.6.1, а). Одну из них замкнем на гальванометр, а др будем подключ к ист тока при помощи ключа К. В мом замыкания (или разм) цепи ключом К гальванометр будет давать показания, т.е. в цепи 2 катушки будет возникать эл ток, первая катушка электрически влияет на вторую. Теперь катушка 1 постоянно подключена к ист, зн ток в ней неизменен. Однако в процессе смещения катушек друг относит др гальванометр дает показания, т.е. причиной появл тока в кат 2 явл измен магн поля, в кот она находилась. Первая катушка заменяется пост магнитом. Результаты опыта при смещении магнита отн кат 2 аналогичны предыд.Причиной всех эл явл в кат 2 явл поведение магн поля, в кот она помещена. Наблюд-ое явл Фар назвал электромагн индукц, т.е. явл-ем возник-ия ЭДС индукц (а также индукционного тока в замкн контуре) при любом изменен магнит потока через площадь, огранич контуром.
Направление индукционного тока в контуре таково, что своим магнитнполем он компенсирует изменен магнитн потока, вызвавшего его появление (правило Ленца). 1 способ (на основе закона сохранения энергии).
где
откуда сила тока в контуре
Поскольку, согласно закону Ома, числитель последнего выражения должен определять суммарную ЭДС в контуре, то, следовательно, второе слагаемое выражает ЭДС индукции, возникшую в нем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 .
.
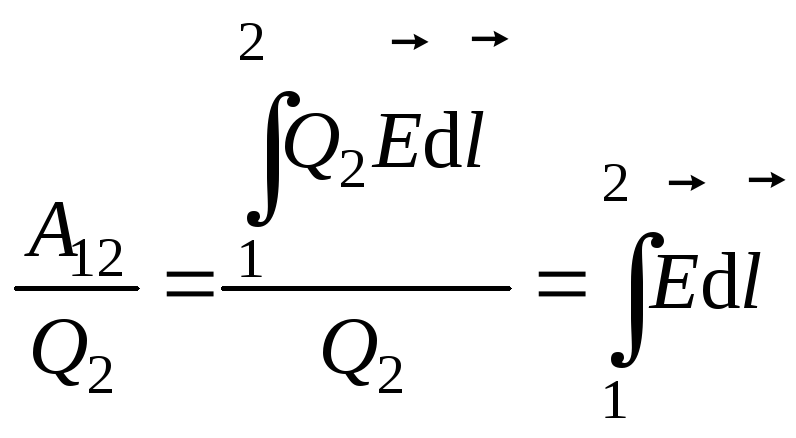 .Разностью
потенциалов между
двумя точками электростат поля наз
отнош работы сил поля по перемещ
пробного электр заряда из одной точки
в другую к величине этого заряда:
.Разностью
потенциалов между
двумя точками электростат поля наз
отнош работы сил поля по перемещ
пробного электр заряда из одной точки
в другую к величине этого заряда: .
.
 .
потенциал
люб точ электрост поля численно равен
раб, соверш силами поля при перемещ
единичн положит заряда из этой точки
в ту, где потенциал поля условно принят
равным нулю.
.
потенциал
люб точ электрост поля численно равен
раб, соверш силами поля при перемещ
единичн положит заряда из этой точки
в ту, где потенциал поля условно принят
равным нулю.

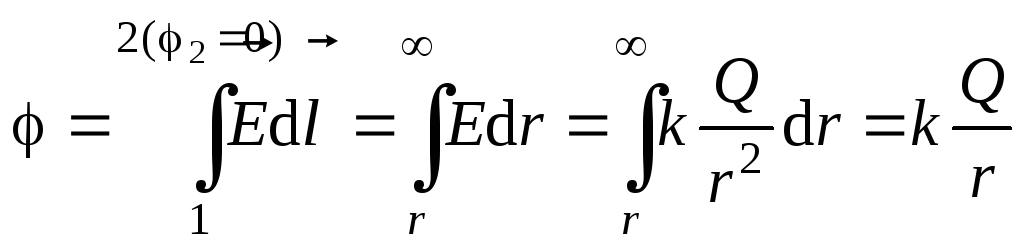 .
.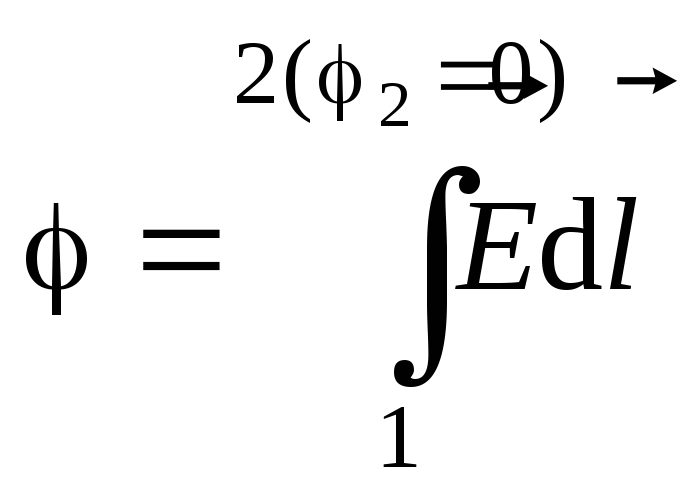 ,
где
,
где
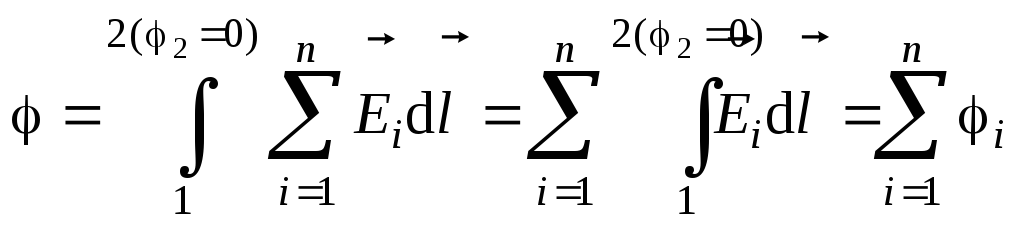 ,
,
 .
.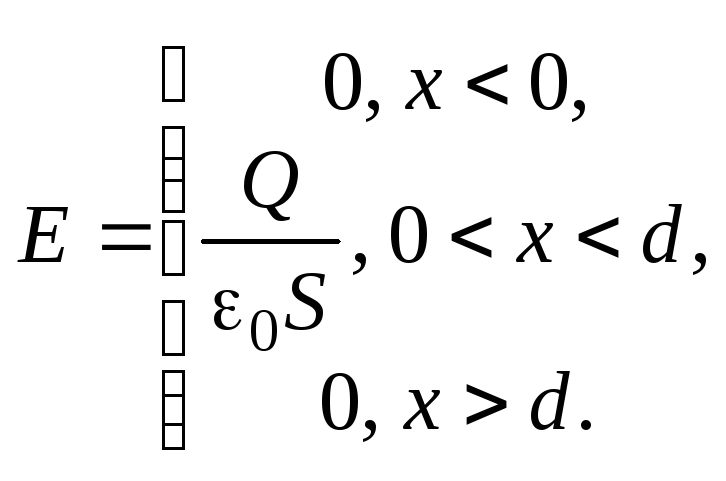


 .
.