3.2. Определение первоначального допустимого базисного решения

В рассмотренном выше примере оптимальное решение получено путем последовательного перехода от первоначального допустимого базисного решения к следующему, "лучшему", и так — до достижения критерия оптимальности. Однако не всегда на первом же шаге получается допустимое базисное решение.

Алгоритм получения первоначального допустимого базисного решения:

1. Если каждая дополнительная переменная входит в уравнение с тем же знаком, что и свободный член, стоящий в правой части уравнения, то дополнительные переменные можно брать в качестве основных на I шаге. При этом получится допустимое базисное решение.

2. Если первое базисное решение получилось недопустимым (например, в качестве основных взяты дополнительные переменные, но хотя бы одна из них входила в уравнение со знаком, противоположным знаку свободного члена), то рассматриваем уравнение, содержащее отрицательный свободный член (любое, если их несколько), и переводим в основные ту неосновную переменную, которая в это уравнение входит с положительным коэффициентом (любую, если их несколько). Такие шаги повторяем до тех пор, пока не достигается допустимое базисное решение.

3. Если базисное решение недопустимое, а в уравнении, содержащем отрицательный свободный член, отсутствует неосновная переменная с положительным коэффициентом, то в этом случае допустимое базисное решение получить невозможно, т.е. условия задачи противоречивы.

В качестве примера рассмотрим задачу о составлении рациона, приведенную в лекции.

Пример 3.2. Решить симплексным методом задачу

при ограничениях:

Решение. Введем дополнительные переменные x₃, x₄, x₅ (каждую со знаком "минус"). Их экономический смысл — это разность между содержанием и необходимым минимумом каждого из питательных веществ.

На I шаге берем дополнительные переменные в качестве основных.

I шаг. Основные переменные: x₃, x₄, x₅.

Неосновные переменные: x₁, x₂.

Выразим основные переменные через неосновные:

X₁ = (0; 0; -9; -8; -12) — первое базисное решение недопустимое, содержащее три отрицательные компоненты. Неосновная переменная x₂ входит в каждое уравнение с положительным коэффициентом, поэтому имеет смысл перевести ее в основные. Возьмем третье уравнение в качестве разрешающего, при этом x₅ = 0 и переходит в неосновные.

II шаг. Основные переменные: x₂, x₄, x₅.

Неосновные переменные: x₁, x₃.

Снова выразим основные переменные через неосновные:

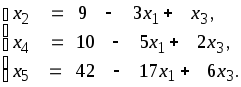
X₂ ⁼ (0; 9; 0; 10; 42) — допустимое базисное решение.

Заканчивая решение задачи симплексным методом (рекомендуем это сделать самостоятельно), на следующем шаге получаем оптимальное базисное решение X₃ = (2; 3; 0; 0; 5), при котором минимальные затраты на рацион составляют F_min = 26. Учитывая экономический смысл исходных и дополнительных переменных, получаем, что в оптимальном рационе используются 2 единицы корма I и 3 единицы корма II, при этом вещества S₁ и S₂ потребляются в необходимых минимальных количествах (x₃ = x₄ = 0), а питательное вещество S₃ оказывается в избытке на 5 единиц (x₅ = 5).

3.3. Особые случаи симплексного метода

Рассмотрим особые случаи, которые могут возникнуть при решении задачи линейного программирования симплексным методом.

1. Появление вырожденного базисного решения. Если на каком-либо шаге наибольшее возможное значение переменной достигается в нескольких строках одновременно (совпадают их оценочные отношения), то разрешающим является любое из них. На следующем шаге получаем вырожденное базисное решение, переход к очередному базисному решению может не изменить функцию цели (F = 0).

2. Отсутствие конечного оптимума (F_max =  или F_min = -). Если на каком-либо шаге получаем, что во всех уравнениях системы бесконечны оценочные отношения той переменной, которая переводится в основные, то задача не имеет конечного оптимума (F_max =  если задача на отыскание максимума, и F_min = – если задача на отыскание минимума).

Подводя итоги, можно утверждать, что если система ограничений непротиворечива, то выполнение конечного числа последовательных шагов симплексного метода либо приводит к нахождению оптимального решения задачи (оно может быть неединственным), либо к установлению того факта, что линейная функция не имеет конечного оптимума.