3. Табличный симплекс-метод

Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (метод последовательного улучшения плана). Суть этого метода в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). При применении этого метода исходная ЗЛП формулируется в канонической форме (1.3).

Симплекс-метод основан на следующих свойствах ЗЛП:

1. Не существует локального экстремума, отличного от глобального. Другими словами: если экстремум есть, то он единственный.

2. Множество всех планов задачи линейного программирования выпукло.

3. Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

4. Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.

Существует две разновидности симплексного метода:

• симплекс-метод с естественным базисом;

• симплекс-метод с искусственным базисом (М-метод);

• Симплекс-метод с естественным базисом.

Для применения этого метода ЗЛП должна быть сформулирована в канонической форме (1.4), причем матрица системы уравнений должна содержать единичную подматрицу размерностью mm . В этом случае очевиден начальный опорный план (неотрицательное базисное решение).

3.1. Алгоритм симплекс – метода

I. Если задача не приведена к каноническому виду, то сделать это так, как в описано в пункте №1. Получить расширенную систему вида:

II. Исходную расширенную систему заносим в первую симплексную таблицу. Последняя строка таблицы, в которой приведено уравнение для линейной функции цели, называется оценочной. В ней указываются коэффициенты функции цели с противоположным знаком: Δ_j =. В левом столбце таблицы записываем основные переменные (базис), в первой строке таблицы — все переменные (отмечая при этом основные), во втором столбце – коэффициенты при основных переменных системы с_i, в третьем столбце – свободные члены расширенной системы b₁, b₂, ..., b_m. Последний столбец подготовлен для оценочных отношений, необходимых при расчете наибольшего возможного значения переменной. В рабочую часть таблицы (начиная с четвертого столбца и второй строки) занесены коэффициенты a_ij при переменных из расширенной системы. Далее таблица преобразуется по определенным правилам.

III. Проверяем выполнение критерия оптимальности при решении задачи на максимум — наличие в последней строке отрицательных коэффициентов Δ_j < 0 (c_i > 0). Если таких нет, то решение оптимально, достигнут max F = (в левом нижнем углу таблицы), основные переменные принимают значения b_i (третий столбец), неосновные переменные равны 0, т.е. получаем оптимальное базисное решение.

IV. Если критерий оптимальности не выполнен, то наибольший по модулю отрицательный коэффициент Δ_j < 0 в последней строке определяет разрешающий столбец s.

Составляем оценочные ограничения каждой строки по следующим правилам:

1. , если b_i и a_is имеют разные знаки;

2. , если b_i = 0 и a_is < 0;

3. , если a_is = 0;

4. 0, если b_i = 0 и a_is > 0;

5. , если a_i0 и a_is имеют одинаковые знаки.

Определяем 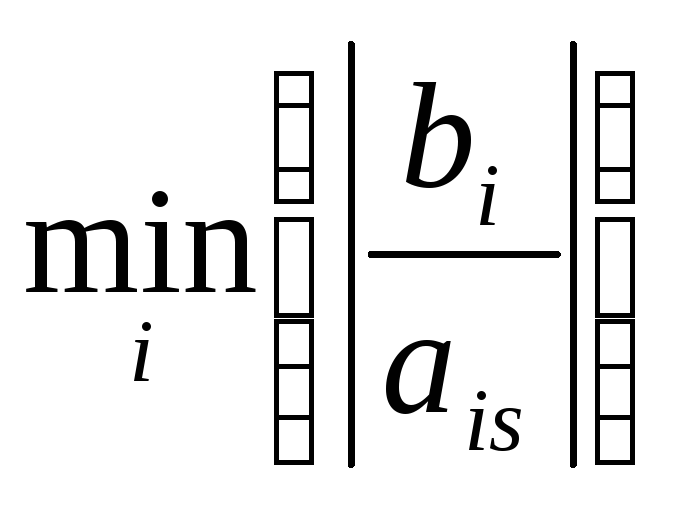. Если конечного минимума нет, то задача не имеет конечного оптимума (Fmax = ). Если минимум конечен, то выбираем строку q, на которой он достигается (любую, если их несколько), и называем ее разрешающей строкой. На пересечении разрешающих строки и столбца находится разрешающий элемент a_qs.

V. Переходим к следующей таблице по правилам:

а) в левом столбце записываем новый базис: вместо основной переменной x_q - переменную x_s,

б) в столбцах, соответствующих основным переменным, проставляем нули и единицы: 1 — против "своей" основной переменной, 0 — против "чужой" основной переменной, 0 — в последней строке для всех основных переменных;

в) новую строку с номером q получаем из старой делением на разрешающий элемент a_qs;

г) все остальные элементы a_qs вычисляем по правилу прямоугольника:

Далее переходим к п. III алгоритма.

Пример 3.1. Решить задачу об использовании ресурсов, приведенную в лекции, с помощью симплексных таблиц.

Решение. Расширенная система задачи имеет вид:

Линейную функцию представим в виде F – 2x₁ - 3x₂ = 0.

Заполняем первую симплексную таблицу (табл. 3.1), в которой переменные x₃, x₄, x₅, x₆ основные. Последняя строка заполняется коэффициентами линейной функции с противоположным знаком (см. п. II алгоритма).

Таблица 3.1

Базис		Коэф. при базисных переменных	Свободный член (План)	Переменные						Оценка
				x1	x2	x3	x4	x5	x6
				2	3	0	0	0	0
x3		0	18	1	3	1	0	0	0	18/3
x4		0	16	2	1	0	1	0	0	16
 x5		0	5	0	1	0	0	1	0	5
x6		0	21	3	0	0	0	0	1	
	F=0*18+0*16+0*5+0*21=0		Δj =	-2	-3	0	0	0	0

В соответствии с п. III алгоритма проверяем критерий оптимальности.

Δ_j = для всех j = 1, 2, ..., 6:

Δ₁ = 0*1+0*2+0*0+0*3 – 2 = – 2

Δ₂ = 0*3+0*1+0*1+0*0 – 3 = – 3

Δ₃ = 0*1+0*0+0*0+0*0 – 0 = 0

Δ₄ = 0*0+0*1+0*0+0*0 – 0 = 0

Δ₅ = 0*0+0*0+0*1+0*0 – 0 = 0

Δ₆ = 0*0+0*0+0*0+0*1 – 0 = 0

В последней строке имеются отрицательные коэффициенты. Выбираем из них наибольший по модулю (Δ₂ = –3); второй столбец разрешающий, переменная x₂ перейдет в основные (этот столбец отмечен рамочкой). В соответствии с п. IV находим оценочные отношения и min{18/3; 16; 5; } = 5. Третья строка является разрешающей (отмечена горизонтальной стрелкой и рамочкой). На пересечении разрешающих строки и столбца стоит разрешающий элемент a₁₁ = 1.

Строим табл. 2 по правилам п. V алгоритма:

а) в новом базисе основные переменные: x₃, x₄, x₂, x₆;

б) расставляем нули и единицы; например, в клетке, соответствующей основной переменной x₃ по столбцу и строке, ставим 1, а в клетке, соответствующей основной переменной x₃ по строке, а основной переменной x₂ — по столбцу, ставим 0 и т.п. В последней строке против всех основных переменных ставим 0. Третья строка получается делением на разрешающий элемент a₁₁ = 1. Остальные клетки заполняем по правилу прямоугольника. Например: , и т.д.

Получим вторую симплексную таблицу (табл. 3.2)

Таблица 3.2

Базис	Коэф. при базисных переменных	Свободный член	Переменные						Оценка
			x1	x2	x3	x4	x5	x6
			2	3	0	0	0	0
 x3	0	3	1	0	1	0	-3	0	3
x4	0	11	2	0	0	1	-1	0	11/2
→ x2	3	5	0	1	0	0	1	0	
x6	0	21	3	0	0	0	0	1	7
	F=0*3+0*11+3*5+0*21=15	Δj =	-2	0	0	0	3	0

Δ_j = для всех j = 1, 2, ..., 6:

Δ₁ = 0*1+0*2+3*0+0*3 – 2 = – 2

Δ₂ = 0*0+0*0+3*1+0*0 – 3 = 0

Δ₃ = 0*1+0*0+3*0+0*0 – 0 = 0

Δ₄ = 0*0+0*1+3*0+0*0 – 0 = 0

Δ₅ = 0*(-3)+0*(-1)+3*1+0*0 – 0 = 3

Δ₆ = 0*0+0*0+3*0+0*1 – 0 = 0

Критерий оптимальности вновь не выполнен (Δ₁ <0). Теперь первый столбец разрешающий; x₁ — переходит в основные, min{3/l; 11/2; ; 7}= 3; первая строка разрешающая, a₁₁ — разрешающий элемент.

Новая симплексная таблица примет вид табл. 3.3.

Таблица 3.3

Базис	Коэф. при базисных переменных	Свободный член	Переменные						Оценка
			x1	x2	x3	x4	x5	x6
			2	3	0	0	0	0
→ x1	2	3	1	0	1	0	-3	0	
 x4	0	5	0	0	-2	1	5	0	5/5
x2	3	5	0	1	0	0	1	0	5/1
x6	0	12	0	0	-3	0	9	1	12/9
	F=2*3+0*5+3*5+0*12=21	Δj =	0	0	2	0	-3	0

Δ_j = для всех j = 1, 2, ..., 6:

Δ₁ = 2*1+0*0+3*0+0*0 – 2 = 0

Δ₂ = 2*0+0*0+3*1+0*0 – 3 = 0

Δ₃ = 2*1+0*(-2)+3*0+0*(-3) – 0 = 0

Δ₄ = 2*0+0*1+3*0+0*0 – 0 = 0

Δ₅ = 2*(-3)+0*5+3*1+0*9 – 0 =-6 + 3=-3

Δ₆ = 2*0+0*0+3*0+0*1 – 0 = 0

И на этот раз критерий оптимальности не выполнен (Δ₅ <0); пятый столбец и вторая строка разрешающие, a₂₅ = 5 — разрешающий элемент.

Переходим к табл. 3.4

Таблица 3.4

Базис	Коэф. при базисных переменных	Свободный член	Переменные						Оценка
			x1	x2	x3	x4	x5	x6
			2	3	0	0	0	0
x1	2	6	1	0	-1/5	3/5	0	0
x5	0	1	0	0	-2/5	1/5	1	0
x2	3	4	0	1	2/5	-1/5	0	0
x6	0	3	0	0	3/5	-9/5	0	1
	F=2*6+0*11+3*4+0*3=24	Δj =	0	0	4/5	3/5	0	0

Δ_j = для всех j = 1, 2, ..., 6:

Δ₁ = 2*1+0*0+3*0+0*0 – 2 = 0

Δ₂ = 2*0+0*0+3*1+0*0 – 3 = 0

Δ₃ = 2*(-1/5)+0*(-2/5)+3*2/5+0*3/5 – 0 = 4/5

Δ₄ = 2*(3/5)+0*1/5+3*(-/5)+0*(-9/5) – 0 = 3/5

Δ₅ = 2*0+0*1+3*0+0*0 – 0 = 0

Δ₆ = 2*0+0*0+3*0+0*1 – 0 = 0

Критерий оптимальности выполнен (все Δ_j > 0), значит F_max ⁼ 24, оптимальное базисное решение (6; 4; 0; 0; 1; 3).