6.5. Оценка точности модели

Для оценки точности модели используйте стандартную ошибку оценки прогнозируемого показателя (или среднеквадратическое отклонение от линии тренда)

, (6.3)

где n- число опытов, m- число факторов, включенных в модель, и среднюю относительную ошибку аппроксимации Если ошибка Е_отн не превышает 15%, то точность модели считается приемлемой. В общем случае допустимый уровень точности, а, значит, и надежности прогноза, устанавливает пользователь модели, который в результате содержательного анализа проблемы выясняет, насколько она чувствительна к точности решения и насколько велики потери из-за неточного решения.

6.6. Построение прогнозов

Если в ходе проверки разрабатываемая модель признана значимой, достаточно точной, и ее качество нас устраивает, то на ее основе разрабатывается точечный прогноз. Он получается путем подстановки в модель значений времени t, соответствующих периоду упреждения k (количество шагов прогноза): t=n+k. Так в случае трендовой модели в виде полинома первой степени – линейной модели роста (6.1) – экстраполяция на k шагов вперед имеет вид:

(6.4)

Для учета случайных колебаний при прогнозировании рассчитываются доверительные интервалы, зависящие от стандартной ошибки (6.3), периода упреждения k, длины временного интервала n и уровня значимости прогноза α. В частности, для прогноза (6.4) будущие значения с вероятностью (1–α) попадут в интервал:

где .

Пример 6.1. В качестве примера рассмотрим разработку трендовой модели и получение прогнозных оценок динамики ВВП России на основе реального временного ряда, представленного в табл. 6.1.

Таблица 6.1

Динамика ВВП России

№	Дата	ВВП (млр. руб.)
1	1.99	238
2	2.99	249
3	3.99	287
4	4.99	340
5	5.99	342
6	6.99	373
7	7.99	360
8	8.99	380
9	9.99	403
10	10.99	419.08
11	11.99	451
12	12.99	460
13	1.00	379.8

Требуется:

1. сгладить Y(t) с помощью простой скользящей средней;

2. определить наличие тренда Y(t);

• с помощью критерия Фишера при α=5% уровне значимости. Для получения критического значения воспользуйтесь функцией FРАСПОБР(; n₁; n₂).

• с помощью критерия Стьюдента при α=5% уровне значимости. Для получения критического значения воспользуйтесь функцией CTЬЮДРАСПОБР(; n₁ + n₂ -2);

3. построить линейную модель Y(t) = а₀ + а₁t, параметры которой оценить МНК;

4. Оценить адекватность построенной модели на основе исследования:

• Случайности остаточной компоненты по критерию пиков;

• Независимости уровней ряда остатков по критерию Дарбина-Уотсона;

• Проверить гипотезу о нормальном распределении остаточной последовательности по R/S_E – критерию;

• Проверить гипотезу о равенстве математического ожидания случайной компоненты нулю на основе t ‑ критерия Стьюдента.

Сделайте вывод об адекватности модели. Модель адекватна, если ВСЕ вышеперечисленные критерии дают положительный ответ.

5. Для оценки точности модели используйте стандартную ошибку оценки прогнозируемого показателя (или среднеквадратическое отклонение от линии тренда) , где n - число опытов, m - число факторов, включенных в модель, и среднюю относительную ошибку аппроксимации

6. Построить точечный прогноз на два периода вперед. Он получается путем подстановки в модель значений времени t, соответствующих времени упреждения k: t=n+k. В случае линейной модели экстраполяция на k шагов вперед имеет вид: _n+k=a₀+a₁*(n+k).

7. Построить доверительный интервал для прогноза, полученного в предыдущем пункте, с вероятностью P=1-=1-0,3=0,7=70% и t=СТЬЮДРАСПРОБР(;n-1):

где .

8. Отобразить на графиках фактические данные, результаты расчетов и прогнозирования.

Решение.

1. Сгладить Y(t) с помощью простой скользящей средней. Выберем интервал сглаживания l=3 и рассчитаем для каждых последующих трех значений .

То есть ,

,

,

,

…

.

Нанесем эти данные на график (см. рис. 6.1)

Рис. 6.1. Исходные данные и скользящая средняя

2. Определить наличие тренда Y(t).

2.1. С помощью критерия Фишера при α=5% уровне значимости.

Разобьем исходный временной ряд y₁, y₂, y₃, …, y_n на две примерно равные по числу уровней части: в первой части n₁=7 первых уровней исходного ряда, во второй — n₂=6 остальных уровней (n₁ + n₂ = n).

Для каждой из этих частей вычисляются средние значения и дисперсии:

;

;

;

Проверим равенство (однородность) дисперсий обеих частей ряда с помощью F-критерия Фишера расчетное значение этого критерия:

Так как , то .

Сравним расчетное значение с критическим, полученным с помощью статистической функции Excel F_крит = FРАСПОБР(; n₁; n₂) = FРАСПОБР(0.05;7;6)=4.2. Так как расчетное значение F_расч меньше критического F_крит (3.256< 4.2), то гипотеза о равенстве дисперсий принимается. Делается вывод о наличии тренда.

2.2. С помощью критерия Стьюдента при α=5% уровне значимости.

проверяется гипотеза об отсутствии тренда с использованием t-критерия Стыодента. Для этого определяется расчетное значение критерия Стыодента по формуле:

где  — среднеквадратическое отклонение разности средних:

.

Для получения критического значения воспользуемся статистической функцией Excel t_крит=CTЬЮДРАСПРОБР(; n₁ + n₂ -2)= CTЬЮДРАСПРОБР(0.05; 11)=2.2. Расчетное значение t больше критического значения статистики Стьюдента t_крит (45.05>2.2), значит с вероятностью р=1-=0,95, гипотеза отвергается, т.е. тренд есть.

В противном случае, если бы t было бы меньше критического, то с заданным уровнем значимости =0,05 сделали бы вывод о том, что тренда нет.

3. Построить линейную модель Y(t) = а₀ + а₁t, параметры которой оценить МНК.

Для того чтобы воспользоваться формулами метода наименьших квадратов (6.2), необходимо произвести промежуточные вычисления, которые расположены в табл. 6.2.

Таблица 6.2

	t	Y	Y*t	t2
	1	238	238	1
	2	249	498	4
	3	287	861	9
	4	340	1360	16
	5	342	1710	25
	6	373	2238	36
	7	360	2520	49
	8	380	3040	64
	9	403	3627	81
	10	419,08	4190,8	100
	11	451	4961	121
	12	460	5520	144
	13	410	5330	169
Сумма	91	4712,08	36093,8	819
Среднее	7	362,47	2776,45	63

Таким образом, искомая модель принимает вид: .

Исходные данные и построенная модель нанесены на график (рис. 6.2)

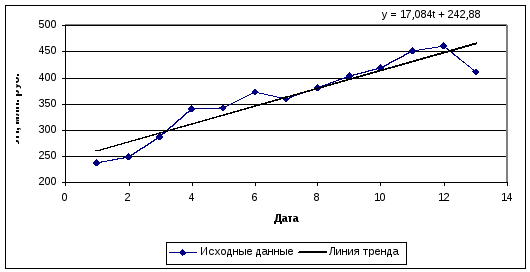
Рис. 6.2. Исходные данные и линия тренда

4. Оценить адекватность построенной модели. Важным этапом прогнозирования социально-экономических процессов является проверка адекватности (соответствия) модели реальному явлению. Для ее осуществления исследуют ряд остатков , то есть отклонений расчетных значений от фактических. Расчеты приведены в табл. 6.3.

В графе 3 приведены расчетные (предсказанные) значения результативного признака (ВВП России), полученные при подстановке фактора t его значений от 1 до 13 в модель . В графе 4 получены остатки вычитанием соответствующих значений элементов графы 3 из графы 2.

Таблица 6.3.

	t	yi		Ei=yi-	пово- ротные точки	(Ei-Ei-1)2	Ei2	Ei*Ei-1
	1	2	3	4	5	6	7	8	9	10
	1	238	259,964	-21,964	-	-	482,417	-	0,0923	36
	2	249	277,048	-28,048	1	37,015	786,690	616,046	0,1126	25
	3	287	294,132	-7,132	0	437,479	50,865	200,038	0,0249	16
	4	340	311,216	28,784	1	1289,959	828,519	-205,287	0,0847	9
	5	342	328,3	13,7	1	227,527	187,69	394,341	0,0401	4
	6	373	345,384	27,616	1	193,655	762,644	378,339	0,0740	1
	7	360	362,468	-2,468	1	905,047	6,091	-68,156	0,0069	0
	8	380	379,552	0,448	0	8,503	0,201	-1,106	0,0012	1
	9	403	396,636	6,364	1	34,999	40,500	2,851	0,0158	4
	10	419,08	413,72	5,36	1	1,008	28,730	34,111	0,0128	9
	11	451	430,804	20,196	1	220,107	407,878	108,251	0,0448	16
	12	460	447,888	12,112	0	65,351	146,7005	244,614	0,0263	25
	13	410	464,972	-54,972	-	4500,263	3021,921	-665,821	0,1341	36
Сумма	91	4712,08	4712,08	-0,004	8	7920,913	6750,847	1038,221	0,6703	182
Среднее	7	362,47	362,47	-0,0003					0,0516

4.1. Для проверки условия случайности возникновения отдельных отклонений от модели часто используется критерий, основанный на поворотных точках. Уровень последовательности E_i считается максимумом, если он больше двух рядом стоящих уровней, т.е. E_{i -1} < E_i > E_{i +1} и минимумом, если он меньше обоих соседних уровней, т.е. E_{i -1} > E_i < E_{i +1}. В обоих случаях E_i считается поворотной точкой (в графе 5 они обозначены 1, иначе 0); общее число поворотных точек для остаточной последовательности E_i обозначим через p=8 (сумма графы 5).

В случайной выборке математическое ожидание числа точек поворота p и дисперсия ²_p выражаются формулами:

Критерием случайности с 5%-ным уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение неравенства , где квадратные скобки означают целую часть числа. Если неравенство выполняется, то с вероятностью 95% делаем вывод о случайном характере ряда остатков. Если это неравенство не выполняется, модель считается неадекватной. Проверим выполнение неравенства:

Так как р=8>4, то с вероятностью 95% делаем вывод о случайном характере ряда остатков.

4.2. Проверка независимости значений уровней случайной компоненты, т.е. проверка отсутствия существенной автокорреляции в остаточной последовательности может осуществляться по ряду критериев, наиболее распространенным из которых является d-критерий Дарбина—Уотсона. Необходимо вычислить расчетное значение 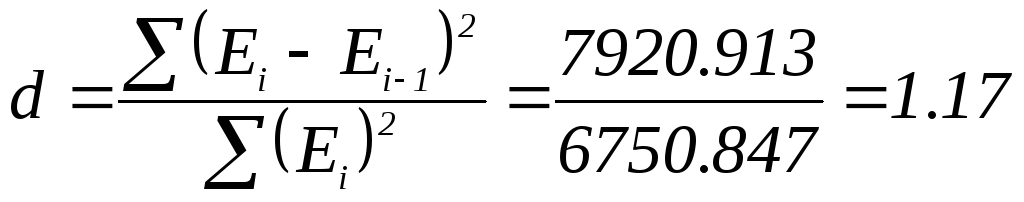, где Е_i – i- тый уровень остаточной последовательности (i=1..13) (расчеты приведены в графах 6 и 7 таблицы 6.3).

Критические границы d₁=1,08 и d₂ =1,36. Так как значение попадает в интервал d₁<d<d₂ (1.08<1.17<1.36) область неопределенности, значит, нет оснований ни принять, ни отвергнуть гипотезу о существовании автокорреляции. Необходимо применять другой критерий. Воспользуемся первым коэффициентом автокорреляции:

.

Сопоставляя это число с табличным значением первого коэффициента автокорреляции 0,485, взятым для уровня значимости α=0,01 и n = 13, увидим, что расчетное значение меньше табличного (0,154<0,485). Это означает, что с ошибкой в 1% ряд остатков можно считать некоррелированным, т. е. свойство взаимной независимости уровней остаточной последовательности подтверждается.

4.3. Проверка гипотезы о нормальном распределении остаточной последовательности по R/S_E – критерию.

В нашем случае

R = E_max ‑ E_min= 28,784 – (– 54,972)=83,756,

где E_max и E_min соответственно максимальный и минимальный уровни ряда остатков;

. Получаем расчетное значение критерия . Для n=13 и α=0,05 найдем критический интервал: [2.92; 4.09]. Так как значение R/S_E попадает в интервал между критическими границами, то с уровнем значимости 5% гипотеза о том, что остаточная последовательность распределена по нормальному закону, принимается.

4.4. Проверка гипотезы о равенстве математического ожидания случайной компоненты нулю на основе t ‑ критерия Стьюдента. Расчетное значение этого критерия задается формулой где — среднее арифметическое значение уровней остаточной последовательности E_i (рассчитано в графе 4); S_E — стандартное (средне-квадратическое) отклонение для этой последовательности. Для получения критического значения t_,v воспользуемся статистической функцией Excel t_,v = CTЬЮДРАСПРОБР(0,05; 12) = 2,16. Так как расчетное значение t меньше критического значения t_,v статистики Стьюдента с заданным уровнем значимости =0,05 и числом степеней свободы v=n-1, то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается.

Так как ВСЕ четыре вышеперечисленные критерии дают положительный ответ, делается вывод о том, что выбранная модель является адекватной реальному ряду экономической динамики.

5. Для оценки точности модели используем стандартную ошибку оценки прогнозируемого показателя (или среднеквадратическое отклонение от линии тренда):

,

где n=13 - число опытов, m=1 - число факторов, включенных в модель (это время t), и среднюю относительную ошибку аппроксимации:

.

Так как ошибка Е_отн не превышает 10%, то точность модели считается приемлемой.

6. Построим точечный прогноз на два периода вперед (k=2). Он получается путем подстановки в модель значений времени t, соответствующих времени упреждения k=2: t=n+k=13+2=15. В случае линейной модели экстраполяция на k шагов вперед имеет вид: _n+k=a₀+a₁*(n+k)=242.88+17.084*15=499.14 (млн. руб.). То есть экстраполяция модели на 2 шага вперед дает прогнозное значение ВВП на март 2000 года, равное 499,14 млн. руб.

7. Построим доверительный интервал для прогноза, полученного в предыдущем пункте, с вероятностью P=1-=1-0,3=0,7=70% и

t=СТЬЮДРАСПРОБР(;n-1).

В этом случае t=СТЬЮДРАСПРОБР(0,3;12)=1,083.

Получим интервальный прогноз:

где .

Таким образом, построенная нами модель является полностью адекватной динамике ВВП и достаточно надежной для краткосрочных прогнозов. Поэтому с вероятностью 70% можно утверждать, что при сохранении сложившихся закономерностей развития значение ВВП, прогнозируемое на март 2000 года с помощью линейной модели роста, попадет в промежуток образованный нижней и верхней границами доверительного интервала .

8. Отобразим на графиках фактические данные, результаты расчетов и прогнозирования (рис. 6.3).

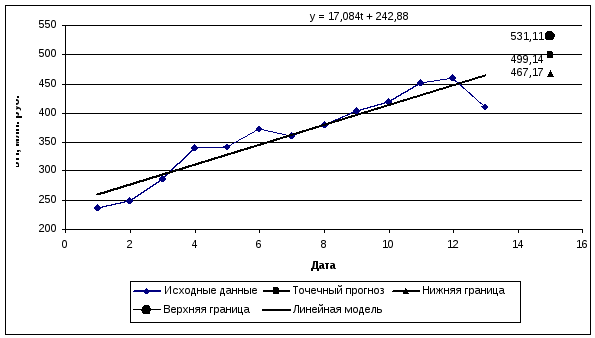
Рис. 6.3. Исходные данные, линейная модель и доверительный интервал для прогноза