2.4. Сплетённые моноидальные категории

В физике существуют процессы, позволяющие «переключать» системы, перемещая их друг относительно друга. В топологии имеется тангл, который описывает процесс переключения двух точек:

Аналогично, в логике можно менять взаимное расположение двух высказываний в конъюнкции — высказывание « и » изоморфно высказыванию « и ». В информатике существует простая программа,  меняющая порядок двух элементов данных. Моноидальная категория, в которой можно производить подобные операции, называется «сплетённой»:

Определение 11. Сплетённая моноидальная категория состоит из:

• Моноидальной категории .

• Естественного изоморфизма, называемого переключателем, который ставит в соответствие каждой паре объектов  изоморфизм .

Данный изоморфизм должен удовлетворять гексагональным условиям:

Первое гексагональное условие предполагает, что переключение объекта  с парой  эквивалентно переключению его сначала с объектом , а затем с объектом  (при использованием ассоциаторов для обработки скобок). Второе условие похоже на первое. Оно утверждает, что переключение пары  также можно провести в два этапа.

В виде струнной диаграммы переключатель  может быть представлен следующим образом:

Обратный морфизм  изображается так:

Данная нотация правильна, поскольку она делает композицию  и  топологически верной:

Гексагональные условия в виде струнных диаграмм:

    В качестве практики читателю рекомендуется доказать следующие равенства:

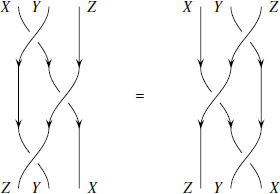
Несколько подсказок в случае возникновения сложностей: первое равенство следует из естественности переключателя. Второе выражение называется равенством Янга-Бакстера и следует из комбинации естественности и гексагональных условий [56].

Далее несколько примеров. Существует множество способов задать в моноидальной категории переключатель. Но в большинстве примеров, приводимых авторами, используются известные «стандартные» переключатели:

• Любая декартова категория автоматически является сплетённой, а в категории  переключатель определяется как .

• В категории  с обычным тензорным произведением стандартный переключатель определяется как .

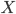• В моноидальной категории  имеется стандартный переключатель , который определяется диффеоморфным к размеченному объединению цилиндров  и . Для категории  (в случае круглых  и ) диаграмма выглядит следующим образом:

• В моноидальной категории  имеется стандартный переключатель для . Для  при  и  в виде единичных точек переключатель выглядит следующим образом:

    Категория иллюстрирует важный принцип. Она является просто категорией, поскольку в нульмерном пространстве вычисления можно производить только «последовательно», то есть при помощи комбинации морфизмов. Категория  является моноидальной, поскольку в одномерном пространстве можно выполнять вычисления «параллельно», то есть при помощи тензорного произведения морфизмов. Категория  является сплетённой моноидальной категорией, поскольку в двумерном пространстве имеется место для перемещения одного объекта вокруг другого. Далее будет показано, что происходит в трёхмерном пространстве или пространстве большей размерности.