2.6. Некоторые свойства расширенных конечных полей

.

Теорема 2.6.1. Среди всех элементов расширенного поля только для элементов основного подполя , т.е. для 0 и 1, выполняется соотношение

.

Доказательство: Справедливость указанного соотношения для нулевого элемента поля очевидна. Среди всех ненулевых элементов поля мультипликативный порядок, равный единице, имеет лишь 1, что и завершает доказательство теоремы.

Теорема 2.6.2.Пусть – конечной поле характеристики . Тогда для любых элементов , , выполняется соотношение

.

Доказательство: Поскольку поле имеет характеристику, равную 2, то сомножитель в разложении бинома обращается в нуль. Следовательно

.

Данная теорема может быть обобщена на случай любого натурального и произвольного числа элементов :

.

Познакомимся теперь с еще одним важным определением.

Пусть . Тогда элементы поля вида

называются 2 – сопряженными с элементом .

Вследствие конечности поля последовательность, составленная из и 2 – сопряженных с ним элементов, имеет ограниченный набор отличающихся друг от друга элементов. Так, если все элементы вида

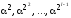
различны, а продолжение последовательности приводит к повторению какого-либо уже содержащегося в ней элемента, то

.

Можно доказать, что длина любой последовательности (цикла) 2–сопряженных элементов поля всегда делит степень расширения .

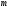Следует отметить, что приведенные выше результаты могут быть обобщены на случай расширения любого недвоичного основного поля .

Раздел 3. Линейные блоковые коды

3.1. Линейные коды

Рассмотрим множество 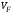, состоящее из всех возможных –компонентных векторов , элементы которого . Очевидно, что образует –мерное векторное пространство. Выберем в этом пространстве линейно независимых векторов , что всегда возможно, поскольку в –мерном пространстве всегда существуют линейно независимых векторов. Построим множество , содержащее векторов, образованных как линейная комбинация вида:

.

Непосредственной проверкой легко убедиться, что множество замкнуто по сложению векторов и умножению их на скаляр из , и, следовательно, является векторным пространством, т.е. подпространством . Это подпространство имеет размерность и непосредственно является той конструкцией, которую назовем линейным кодом.

Двоичным линейным кодом является любое –мерное подпространство пространства векторов длины .

Поскольку подпространство содержит кодовых слов, то есть ни что иное, как число информационных символов, переносимых кодом, а – длина кода. Наряду с обозначением кода как код, встречается и другое, в котором используется еще один его параметр – кодовое расстояние: .

3.2. Определение циклического кода. Порождающий полином

Циклические коды являются подклассом линейных кодов, удовлетворяющие дополнительному структурному требованию. В силу этого требования поиск хороших помехоустойчивых кодов оказался наиболее продуктивным. При этом в качестве математического аппарата используется теория полей Галуа. Вне класса циклических кодов теория полей Галуа не столь эффективна.

Важность циклических кодов обусловлена также тем, что заложенные в основу их построения идеи теории конечных полей приводят к процедурам кодирования и декодирования, эффективным как с алгоритмической, так и вычислительной точек зрения.

Линейный блоковый код длины называется циклическим, если наряду с любым своим кодовым словом он содержит также циклический сдвиг этого слова. Иными словами, циклический код содержит все циклические сдвиги всех своих кодовых слов.

Лемма 3.2.1. Пусть некоторому слову циклического кода сопоставлен полином 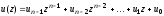. Тогда его циклическому сдвигу будет соответствовать полином , являющийся вычетом полинома по модулю бинома , т.е. .

Доказательство: Добавим и вычтем в соотношении для и сгруппируем его слагаемые следующим образом

.

Откуда непосредственно следует утверждение леммы 3.2.1.

На основании леммы 3.2.1. не составляет труда показать, что –кратному циклическому сдвигу слова будет соответствовать полином , определяемый как

. (**)

Лемма 3.2.2. Если – кодовый полином слова циклического кода , то для произвольного полинома вычет произведения по модулю биномa также является кодовым полиномом.

Доказательство: Пусть , где . Тогда

.

Отсюда на основании леммы 3.2.1, ясно, что каждое слагаемое последнего выражения является кодовым полиномом, отвечающим некоторому циклическому сдвигу исходного слова 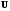. Учитывая же свойства линейного подпространства, т.е. тот факт, что умножение на скаляр и сложение кодовых слов вновь дают кодовое слово, следует, что вычет по модулю также соответствует кодовому слову.

Следствие. Если степень полинома удовлетворяет неравенству

,

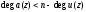то само произведение отвечает полиному некоторого слова циклического кода.

Рассмотрим множество полиномов 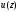, образующих циклический код и найдем среди них ненулевой полином наименьшей степени.

Ненулевой нормированный кодовый полином циклического кода наименьшей степени называется порождающим многочленом циклического кода.

Следовательно, если , то .

Теорема 3.2.1. Любой кодовый полином циклического кода делится без остатка на порождающий многочлен этого кода, т.е.

Доказательство: Предположим противное, т.е. что существует некоторый кодовый многочлен, который представим в виде

,

где остаток от деления на.

Так как , то, согласно следствию из леммы 3.2.2, многочлен 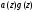является кодовым. Тогда, с учетом линейности кода, также является кодовым многочленом. Но поскольку , то в циклическом коде содержится кодовый полином, имеющий меньшую степень, чем порождающий, что противоречит определению порождающего полинома, а значит, наше предположение неверно, и порождающий многочлен делит без остатка любой кодовый полином, т.е. .

Таким образом, любой кодовый полином циклического кода может быть представлен в виде произведения

,

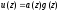в котором – порождающий многочлен, а – некоторый информационный полином. Иными словами, отличие всех кодовых полиномов друг от друга определяется только информационными полиномами. Поскольку

,

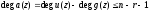то для двоичных кодов может существовать различных информационных полиномов , т.е. различных кодовых слов. Отсюда число информационных символов в каждом кодовом слове , и, значит, , тогда как степень порождающего многочлена

соответствует числу проверочных символов.

Порождающий многочлен циклического кода обладает характерными чертами, которые устанавливается следующей теоремой.

Теорема 3.2.2. Порождающий многочлен 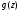циклического кода длины обязательно делит бином .

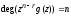Доказательство: Из леммы 3.2.1 следует, что вычет из произведения по модулю является кодовым полиномом. Учитывая, что , то

,

и значит, как кодовый полином, делится без остатка на. Следовательно, и делится на .