
- •Введение
- •В дипломной работе рассмотрен спектральный метод кодирования кодов Рида-Соломона над полем gf(). В основе спектрального описания рс-кодов лежит дискретное преобразование Фурье (дпф над конечным полем.
- •Раздел 1. Основы теории помехоустойчивого кодирования
- •1.1 Основные определения
- •1.2 Классификация кодов
- •1.3 Принципы обнаружения и исправления ошибок
- •1.4. Корректирующая способность кода
- •Раздел 2. Арифметика и структура конечных полей галуа. Многочлены над полями галуа
- •2.1. Введение в теорию конечных полей
- •2.2 Векторное пространство над конечными полями. Линейная зависимость и независимость
- •2.3 Арифметика полиномов, заданных над конечным полем
- •2.4. Расширенные конечные поля
- •2.5 Мультипликативный порядок элементов поля. Примитивные элементы. Другой подход к построению расширения поля Галуа
- •2.6. Некоторые свойства расширенных конечных полей
- •Раздел 3. Линейные блоковые коды
- •3.1. Линейные коды
- •3.2. Определение циклического кода. Порождающий полином
- •3.3. Систематический циклический код
- •3.4. Коды Рида-Соломона
- •Раздел 4. Спектральное описание циклических кодов
- •4.1. Дискретное преобразование Фурье
- •4.2. Китайская теорема об остатках
- •4.3. Трехмерное преобразование Фурье в поле
- •4.4 Быстрое преобразование Фурье бпф длины 3
- •4.5. Быстрое преобразование Фурье длины 5
- •4.6 Быстрое преобразование Фурье длины 17
- •4.8. Несистематические бпф-укорочения
- •Заключение
- •Список использованной литературы
- •Приложения Приложение 1. Анализ временных характеристик кодера кодов Рида-Соломона
- •Приложение 2 Листинг программы
1.3 Принципы обнаружения и исправления ошибок
Пусть для передачи
сообщений используется некоторый код
длины
 и объема
и объема
 .
Это означает, что на вход дискретного
канала поступает одна из последовательностей
.
Это означает, что на вход дискретного
канала поступает одна из последовательностей ,
называемая кодовым словом. На приемной
стороне наблюдается некоторая выходная
последовательность (вектор наблюдений)
,
называемая кодовым словом. На приемной
стороне наблюдается некоторая выходная
последовательность (вектор наблюдений)
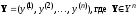 .
Процедуру решения о том, произошла ли
ошибка при передаче кодовой
последовательности или нет, можно
описать следующим алгоритмом. Все
множество
.
Процедуру решения о том, произошла ли
ошибка при передаче кодовой
последовательности или нет, можно
описать следующим алгоритмом. Все
множество
 разбивается на две области
разбивается на две области
 и
и
 ,
причем область
,
причем область
 образована кодовыми последовательностями,
а
образована кодовыми последовательностями,
а
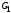 – запрещенными комбинациями. Очевидно,
что если наблюдаемая последовательность
– запрещенными комбинациями. Очевидно,
что если наблюдаемая последовательность
 ,
полученная в результате трансформации
каналом некоторой кодовой комбинации
,
полученная в результате трансформации
каналом некоторой кодовой комбинации
 ,
оказывается в области
,
оказывается в области
 ,
то принимается решение об обнаружении
ошибок в принятой последовательности.
Если же наблюдаемая последовательность
окажется в области
,
то принимается решение об обнаружении
ошибок в принятой последовательности.
Если же наблюдаемая последовательность
окажется в области
 ,
то принимается решение о безошибочной
передаче информации.
,
то принимается решение о безошибочной
передаче информации.
Естественно
возникает вопрос о том, а все ли ошибки
могут быть обнаружены? Предположим, что
алфавит входных
 и выходных
и выходных
 символов одинаков, и его объем равен
символов одинаков, и его объем равен
 .
Тогда объем кода, а значит и мощность
множества
.
Тогда объем кода, а значит и мощность
множества
 ,
составляют величину
,
составляют величину
 ,
а число запрещенных комбинаций (или
мощность множества
,
а число запрещенных комбинаций (или
мощность множества
 )
определится как
)
определится как
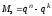 .
При передаче по каналу связи M
кодовых комбинаций возможны
.
При передаче по каналу связи M
кодовых комбинаций возможны
 их переходов в принятые наблюдения
их переходов в принятые наблюдения
 ,
из которых только
,
из которых только
 будут правильными, тогда как остальные
будут правильными, тогда как остальные
 переходов сопровождаются искажениями.
Как уже указывалось, решение об обнаружение
ошибок в принятой последовательности
принимается всякий раз, когда она
оказывается в области
переходов сопровождаются искажениями.
Как уже указывалось, решение об обнаружение
ошибок в принятой последовательности
принимается всякий раз, когда она
оказывается в области
 .
Подобной ситуации отвечают
.
Подобной ситуации отвечают
 переходов и, значит, общее число
обнаруживаемых ошибок составляет
величину
переходов и, значит, общее число
обнаруживаемых ошибок составляет
величину
 ,
что еще раз свидетельствует о возможности
обнаружения ошибок только при условии
,
что еще раз свидетельствует о возможности
обнаружения ошибок только при условии
 ,
т.е. при введении избыточных символов.
Сравнение же общего количества ошибок
,
т.е. при введении избыточных символов.
Сравнение же общего количества ошибок с числом обнаруживаемых
с числом обнаруживаемых
 демонстрирует, что не все ошибки удается
зафиксировать. Последнее объясняется
тем, что переход одной кодовой комбинации
в другую под действием канальных помех
невозможно обнаружить, причем общее
количество подобных переходов составит
величину
демонстрирует, что не все ошибки удается
зафиксировать. Последнее объясняется
тем, что переход одной кодовой комбинации
в другую под действием канальных помех
невозможно обнаружить, причем общее
количество подобных переходов составит
величину
 .
.
Аналогичным
образом реализуется и процедура
исправления ошибок. Отличие заключается
лишь в том, что все множество
 разбивается теперь на
разбивается теперь на
 (по числу передаваемых сообщений)
решающих областей
(по числу передаваемых сообщений)
решающих областей

 ,
причем
,
причем
 и
и
 при
при не пересекаются, а в каждую область
решения
не пересекаются, а в каждую область
решения
 включается только одна кодовая
последовательность. Если оказывается,
что вектор наблюдений
включается только одна кодовая
последовательность. Если оказывается,
что вектор наблюдений
 принадлежит j-й
области, т.е.
принадлежит j-й
области, т.е.
 ,
то принимается решение о том, что было
передано слово
,
то принимается решение о том, что было
передано слово
 и, значит, канальные ошибки, вызвавшие
трансформацию
и, значит, канальные ошибки, вызвавшие
трансформацию
 в
в ,
будут исправлены. Поскольку области
решений не перекрываются, то общее число
исправляемых ошибок определяется числом
запрещенных комбинаций, распределяемых
между M
решающими областями. Следовательно,
,
будут исправлены. Поскольку области
решений не перекрываются, то общее число
исправляемых ошибок определяется числом
запрещенных комбинаций, распределяемых
между M
решающими областями. Следовательно,
 и, значит, как и в случае обнаружения
ошибок, их исправление возможно лишь
при
и, значит, как и в случае обнаружения
ошибок, их исправление возможно лишь
при
 ,
т.е. при введении избыточности.
,
т.е. при введении избыточности.
1.4. Корректирующая способность кода
Для того, чтобы дать наглядное, геометрическое толкование процедуры различения сигналов, введем понятие расстояния Хэмминга.
Расстояние
Хэмминга ,
определяется как число позиций, в которых
кодовые символы двух слов отличаются
друг от друга.
,
определяется как число позиций, в которых
кодовые символы двух слов отличаются
друг от друга.
Данная характеристика показывает, насколько удалены сигналы друг от друга, что играет определяющую роль в теории информации в целом. Чем больше расстояние между сигналами, тем меньше вероятность перепутывания переносимой ими информации.
Для расстояния Хэмминга выполняются следующие три аксиомы:
– симметрии –
 ;
;
– неотрицательности
–
 ,
причем если
,
причем если
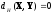 ,
то
,
то
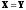 ;
;
– неравенства
треугольника –
 .
.
Наряду с расстоянием
Хэмминга широко используется такая
характеристика, как вес
Хэмминга .
Весом Хэмминга вектора
.
Весом Хэмминга вектора
 называется число его ненулевых компонент.
Очевидно, что
называется число его ненулевых компонент.
Очевидно, что
 и
и
 ,
где под суммированием векторов понимается
покомпонентное сложение.
,
где под суммированием векторов понимается
покомпонентное сложение.
Пример
1.4.1. Для двух
двоичных векторов
 и
и
 расстояние Хэмминга
расстояние Хэмминга
 ,
поскольку символы, стоящие на второй,
третьей и пятой позиций различаются, а
на первой и четвертой – совпадают. В
свою очередь вес Хэмминга для указанных
векторов составляет величину
,
поскольку символы, стоящие на второй,
третьей и пятой позиций различаются, а
на первой и четвертой – совпадают. В
свою очередь вес Хэмминга для указанных
векторов составляет величину
 и
и
 .
.
Теорема 1.4.1. Код
исправляет любые ошибки кратности
 и менее в том и только в том случае, если
кодовое расстояние удовлетворяет
неравенству
и менее в том и только в том случае, если
кодовое расстояние удовлетворяет
неравенству
 . (*)
. (*)
Доказательство:
Достаточность:
Пусть
имеется код
 с кодовым расстоянием
с кодовым расстоянием
 .
Предположим, что произошла ошибка
кратности
.
Предположим, что произошла ошибка
кратности
 ,
и что найдутся два кодовых вектора
,
и что найдутся два кодовых вектора
 и
и
 такие, что
такие, что
 ,
,
а
значит, не позволяющие исправить ошибку
кратности
 .
Однако, как следует из аксиом расстояния,
.
Однако, как следует из аксиом расстояния,
 ,
,
что
противоречит условию теоремы.
Следовательно, неравенство (*) определяет
достаточное условие исправление ошибок
кратности
 и менее.
и менее.
Необходимость:
С другой
стороны, если
 ,
то обязательно возникнет ситуация, при
которой произойдет неверное декодирование.
Например, если
,
то обязательно возникнет ситуация, при
которой произойдет неверное декодирование.
Например, если
 ,
то существует такой вектор наблюдения
,
то существует такой вектор наблюдения
 ,
для которого
,
для которого
 ,
и, следовательно, наблюдается
неопределенность в принятии решения.
Таким образом, условие (*) является
необходимым.
,
и, следовательно, наблюдается
неопределенность в принятии решения.
Таким образом, условие (*) является
необходимым.
Полезной иллюстрацией
приведенного доказательства может
служить диаграмма, представленная на
рис. 1. На ней изображены сферы
Хэмминга радиуса
 c
центром
c
центром
 ,
представляющие собой множество точек
(векторов), расположенных от
,
представляющие собой множество точек
(векторов), расположенных от на
расстоянии Хэмминга
на
расстоянии Хэмминга
 или ближе. Если все сферы Хэмминга
радиуса
или ближе. Если все сферы Хэмминга
радиуса
 ,
окружающие кодовые вектора
,
окружающие кодовые вектора
 ,
не перекрываются, декодер воспримет
любой вектор внутри i–ой
сферы, как i–ый
кодовый вектор
,
не перекрываются, декодер воспримет
любой вектор внутри i–ой
сферы, как i–ый
кодовый вектор
 .
Это означает, что любая ошибка кратности
.
Это означает, что любая ошибка кратности
 и менее в кодовом слове будет исправлена.
Вместе с тем, при условии исправления
любых ошибок кратности
и менее в кодовом слове будет исправлена.
Вместе с тем, при условии исправления
любых ошибок кратности
 избежать перекрытия сфер можно только
в том случае, если минимальное расстояние
Хэмминга между кодовыми векторами не
меньше, чем
избежать перекрытия сфер можно только
в том случае, если минимальное расстояние
Хэмминга между кодовыми векторами не
меньше, чем
 .
.
Из представленной
диаграммы легко увидеть, что обнаружение
ошибок кратности
 в принятых векторах возможно тогда,
когда выполняется условие
в принятых векторах возможно тогда,
когда выполняется условие
 .
.
Из
рассмотренного видно, что основными
параметрами блокового кода являются:
кодовое расстояние
![]() ,
его объем
,
его объем
 и длина
и длина
 .
Часто при описании характеристик кода
вместо объема
.
Часто при описании характеристик кода
вместо объема
 используют либо число информационных
символов в кодовом слове
используют либо число информационных
символов в кодовом слове
![]() ,
либо скорость кода
,
либо скорость кода
 .
Именно с этими параметрами связаны два
основных варианта задач, рассматриваемых
теорией кодирования. Первая из них
связана с максимизацией
.
Именно с этими параметрами связаны два
основных варианта задач, рассматриваемых
теорией кодирования. Первая из них
связана с максимизацией
![]() при заданных значениях
при заданных значениях
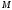 (
( или
или
 )
и
)
и
 для достижения хорошей корректирующей
способности кода. Дуальной задачей
является максимизация
для достижения хорошей корректирующей
способности кода. Дуальной задачей
является максимизация
 (
( или
или![]() )
при минимуме
)
при минимуме
![]() и длины
и длины
 .
.
