4.4 Быстрое преобразование Фурье бпф длины 3

3-точечное ДПФ с ядром β для вектора задается формулой

)=

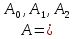Так как ядро β удовлетворяет тождеству 1+, то легко проверить непосредственно, что числа могут быть вычислены по правилу:

, которое содержит только одно умножение и 5 сложений (вместо 4 умножений и 6 сложений). Если , .

4.5. Быстрое преобразование Фурье длины 5

5-точечное ДПФ с ядромзадается равенством

,

непосредственное вычисление по которому требует 16 умножений и 20 сложений. Использование только тождества на ядре (которое в данном случае имеет вид 1+++) дает 9 умножений и 21 сложение. Это достигается, например, следующим образом:

,

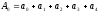Аналогично,

,

,

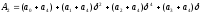и, наконец,

Дальнейшего уменьшения числа умножений можно добиться за счет перехода к циркулянту и использования полиномиальной свертки (ПС). Приведем необходимые сведения:

Утверждение 4.5.1. Два двучлена 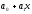и , , , , 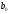, можно перемножить, выполняя не более трех умножений чисел в поле F.

Действительно, ()()≜, где , и

Если умножение происходит в поле F, то , где ,

Следствие 4.5.1. Два многочлена степени m над полем F можно перемножить, выполняя не более умножений чисел в поле F.

Например, для m=3 (с учетом, что char GF()=2) имеем:

₍₁₀₎

≜≜=

≜

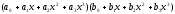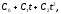
где t≜ (так что при вычислении по модулю многочлена надо делать редукцию по модулю ); согласно утверждению 4.5.1:

≜

≜

≜

Для вычисления , , опять воспользуемся утверждением 4.5.1. Имеем

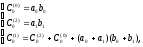
₍₁1)

Таким образом, для вычисления коэффициентов многочлена необходимо только 9 (вместо 16) умножений. Точные формулы для коэффициентов многочлена (при ) имеют вид:

₍₁2)

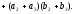
Для коэффициентов при, согласно (10)-(12)

,

,

,

,

₍₁3)

,

,

,

Если произведение вычисляется в кольце F(так что 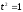), то формулы (10)-(12) принимают вид:

≜, (10а)

(11a)

, ≜

,

.

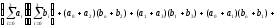
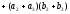Вычисление вектора гдеа – циркулянт, первая строка которого задается вектором , равносильно вычислению в F произведения , где и .

Подчеркнем, что преобразуемая последовательность , за исключением первого элемента, дает реверсивный порядок коэффициентов многочлена при 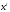координате стоит коэффициент .

Утверждение 4.5.2. Для ДПФ простой длины n всегда существует такая перестановка строк и столбцов матрицы Фурье, что она может быть превращена в окаймленный циркулянт.

Этот результат принадлежит Рейдеру. Мы подробно проиллюстрируем соответствующий алгоритм в следующем пункте, посвященному БПФ длины 17, а сейчас вернемся к БПФ длины 5.

Прежде всего избавимся от единичного окаймления матрицы Фурье:

= )

В столбцах и строках матрицы, стоящей в правой части равенства выполним перестановку . Если выполним такую же перестановку координат у векторов d и его спектра А, получаем

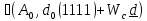) (14)

Циркулярная матрица для БПФ длины 5 получается, если задать нумерацию ненулевого элемента поля GF(5) с образующей 3: 1 (mod5), 33 (mod5), 4 (mod5), 2 (mod5): .

Этим задача свелась, согласно утверждения 4.5.2, к вычислению многочлена c(x)=d(x)w(x)mod(x-1), где d(x)=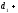 или, иначе, циклической свертки с=с

Для вычисления этой циклической свертки длины 4, перепишем формулы (13) в более удобном для организации экономного вычисления виде:

, ;

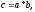
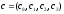(15)

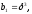
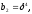
Этот алгоритм содержит 9 умножений и 17 сложений. Но если появляются какие-то условия на коэффициенты или,то число вычислений уменьшается. Например, если =0 или 1, то число умножений равно только 5. В нашем случае 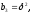и так как - ядро БПФ длины 5, то=1. Учитывая это, из формул (13) – (14) окончательно приходим к следующему алгоритму:

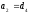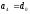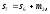
, , , , , , , , , , , . (16)

Так что алгоритм БПФ длины 5 в поле в нашем случае содержит 5 умножений и 11сложений.