
- •Введение
- •В дипломной работе рассмотрен спектральный метод кодирования кодов Рида-Соломона над полем gf(). В основе спектрального описания рс-кодов лежит дискретное преобразование Фурье (дпф над конечным полем.
- •Раздел 1. Основы теории помехоустойчивого кодирования
- •1.1 Основные определения
- •1.2 Классификация кодов
- •1.3 Принципы обнаружения и исправления ошибок
- •1.4. Корректирующая способность кода
- •Раздел 2. Арифметика и структура конечных полей галуа. Многочлены над полями галуа
- •2.1. Введение в теорию конечных полей
- •2.2 Векторное пространство над конечными полями. Линейная зависимость и независимость
- •2.3 Арифметика полиномов, заданных над конечным полем
- •2.4. Расширенные конечные поля
- •2.5 Мультипликативный порядок элементов поля. Примитивные элементы. Другой подход к построению расширения поля Галуа
- •2.6. Некоторые свойства расширенных конечных полей
- •Раздел 3. Линейные блоковые коды
- •3.1. Линейные коды
- •3.2. Определение циклического кода. Порождающий полином
- •3.3. Систематический циклический код
- •3.4. Коды Рида-Соломона
- •Раздел 4. Спектральное описание циклических кодов
- •4.1. Дискретное преобразование Фурье
- •4.2. Китайская теорема об остатках
- •4.3. Трехмерное преобразование Фурье в поле
- •4.4 Быстрое преобразование Фурье бпф длины 3
- •4.5. Быстрое преобразование Фурье длины 5
- •4.6 Быстрое преобразование Фурье длины 17
- •4.8. Несистематические бпф-укорочения
- •Заключение
- •Список использованной литературы
- •Приложения Приложение 1. Анализ временных характеристик кодера кодов Рида-Соломона
- •Приложение 2 Листинг программы
4.2. Китайская теорема об остатках
Рассмотрим более
детально формулу (4.1), задающую ДПФ над
полем
 .
Например, для того, чтобы вычислить ДПФ
над полем
.
Например, для того, чтобы вычислить ДПФ
над полем
 вектора длины
вектора длины ,
требуется
,
требуется
 умножений в поле. Как известно, умножение
является одной из наиболее затратных
по времени операций, т.е. алгоритм ДПФ
имеет сложность порядка O(
умножений в поле. Как известно, умножение
является одной из наиболее затратных
по времени операций, т.е. алгоритм ДПФ
имеет сложность порядка O( .
Известные алгоритмы многомерного
преобразования Фурье, а так же БПФ
(быстрое преобразование Фурье) позволяют
снизить эту цифру до N*logN
умножений. Данные алгоритмы основаны
на следующей китайской теореме об
остатках.
.
Известные алгоритмы многомерного
преобразования Фурье, а так же БПФ
(быстрое преобразование Фурье) позволяют
снизить эту цифру до N*logN
умножений. Данные алгоритмы основаны
на следующей китайской теореме об
остатках.
Теорема 4.2.1. (Китайская теорема об остатках, единственность)
Для заданного
множества целых положительных попарно
взаимно-простых чисел и
множества неотрицательных целых чисел
и
множества неотрицательных целых чисел

при ,
система сравнений
,
система сравнений

имеет
не более одного решенияc
в интервале
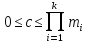
Теорема 4.2.2. (Китайская теорема об остатках, существование)
Пусть
 –произведение
целых положительных попарно взаимно-простых
положительных чисел, пусть
–произведение
целых положительных попарно взаимно-простых
положительных чисел, пусть
 и
пусть
и
пусть
 удовлетворяют
равенству
удовлетворяют
равенству
 ,
тогда единственным решением системы
сравнений
,
тогда единственным решением системы
сравнений

будет

Эта теорема
позволяет каждое число n,0≤n<M
однозначно
задать системой остатков по модулям
 ,
i=1,k.
,
i=1,k.
4.3. Трехмерное преобразование Фурье в поле
Рассмотрим ДПФ
длины N=255,
ядром которого является примитивный
элемент поля
 .
.
(1) 5
5 17,
17,
 =3,
=3,
 =
5,
=
5,
 =17,
так что n
=17,
так что n (
( ,
,
 ,
,
 ),
где
),
где
 ,
,
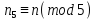 ,
,

(2)
Произвольный
ненулевой элемент
 поля
поля
 )
задается как степень примитивного
элемента
)
задается как степень примитивного
элемента
 поля:
поля:
 =
=
 ,
,

Согласно (2)
(3) =
=
 (
( ,
,
 ,
,
 =
= ,
,
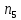 =
= =
= ,
,
Где
приняты обозначения:
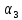 =
= ,
,
 =
= ,
, =
=
Более того, в силу
попарной взаимной простоты модулей
 ,
если i
,
если i (
( ,
,
 ,
,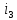 )
и j
)
и j (
( ,
,
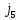 ,
,
 ),
то ij
),
то ij (
( ,
,
 ,
,
 ).
Таким образом, формулу (4.1) определяющую
ДПФ, можно переписать в виде:
).
Таким образом, формулу (4.1) определяющую
ДПФ, можно переписать в виде:
(4)
 ,
,
 =
= ,
,
 =
=
Это сразу подсказывает
следующий алгоритм вычисления вектора
 по вектору
по вектору
 .
Сначала разбиваем координаты вектора
.
Сначала разбиваем координаты вектора
 на тройки чисел (прификсированных
на тройки чисел (прификсированных и
и
 )
и к каждой из них применяем 3-точечное
преобразование с ядром
)
и к каждой из них применяем 3-точечное
преобразование с ядром
 =
= ;
это дает набор из 255 величин
;
это дает набор из 255 величин
(5)
 ,
,
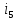 =
= ,
,
 =
= .
.
Затем к этому
вектору
 длины 255 применяется 5-точечное ДПФ с
ядром
длины 255 применяется 5-точечное ДПФ с
ядром
 =
= по правилу: координаты вектора
по правилу: координаты вектора
 группируются по 5 чисел (по фиксированным
группируются по 5 чисел (по фиксированным
 и
и
 )
и для каждой такой совокупности
вычисляется 5-мерный вектор
)
и для каждой такой совокупности
вычисляется 5-мерный вектор
 ,
,
(6)
 ,
,
 =
= ,
,
 =
= .
.
Наконец, к вектору
 длины 255 применяется 17-точечное ДПФ с
ядром
длины 255 применяется 17-точечное ДПФ с
ядром
 =
= ,
приводящее к искомому 255-мерному вектору
,
приводящее к искомому 255-мерному вектору
 :
:
(7)
 ,
,
 =
= ,
,
 =
= .
.
(8) умножений при прямом вычислении по
формуле (4.1) требует
умножений при прямом вычислении по
формуле (4.1) требует

(9)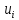 - число умножений, необходимое для
выполнения i-точечного
ДПФ, i=3,5,17.
Аналогично выписывается и формула для
числа сложений (кстати, напомним, что
характеристика рассматриваемого поля
равна 2, так что вычитание совпадает со
сложением)
- число умножений, необходимое для
выполнения i-точечного
ДПФ, i=3,5,17.
Аналогично выписывается и формула для
числа сложений (кстати, напомним, что
характеристика рассматриваемого поля
равна 2, так что вычитание совпадает со
сложением)

Экспериментально установлено, что переход от одномерной структуры к трехмерной, уменьшает время, требуемое на вычисление ДПФ примерно в 10 раз.
Таким образом, переход от ДПФ длины 255 к ДПФ длин 3, 5 и 17, каждое из которых вычисляется 255 раз в цикле, очень существенно понижает вычислительную сложность алгоритма.
Следующий наш шаг
– полностью избавиться от ДПФ внутри
циклов, заменив их на БПФ (быстрое
преобразование Фурье) длин 3, 5 и 17, которые
основаны как на свойствах поля
 ,
так и на свойствах алгоритмов быстрого
умножения многочленов, заданных над
конечным полем.
,
так и на свойствах алгоритмов быстрого
умножения многочленов, заданных над
конечным полем.
