31. Способы задания множеств. Операции над множествами.

Способы:

Множество может быть задано следующими способами: списком его элементов, порождающей процедурой и описанием свойств его элементов.

I. Списком могут быть заданы только конечные множества. ;

этот способ не пригоден для задания бесконечных множеств и даже в случае конечных множеств не всегда практически реализуем.

II. Порождающая процедура описывает способ получения элементов множества из уже полученных элементов; используется для задания бесконечных и конечных множеств. Например, множество порождающая процедура для которого определяется следующими двумя правилами:

1) ;

2) если то .

Правила, описанные таким образом называются индуктивными или рекурсивными.

III. Задание множества описанием свойств его элементов. В случае, когда свойство элементов множества М может быть описано коротким выражением ρ(х), множество М задания при помощи обозначается:

М={хρ(х)}, которое читается так: М – это множество элементов х, обладающих свойством ρ. Вместо вертикальной черты часто используется двоеточие. ρ(х) –это либо высказывание, в котором что-либо утверждается об х, либо это некоторая функция переменной х, например:

С помощью указанных средств не возможно сконструировать все возможные множества. Уже в самом задании конкретного множества явно или неявно ограничивается совокупность допустимых объектов.

Операции:

Множества можно определять также при помощи операций над некоторыми другими множествами.

Пусть имеются два множества: А и В.

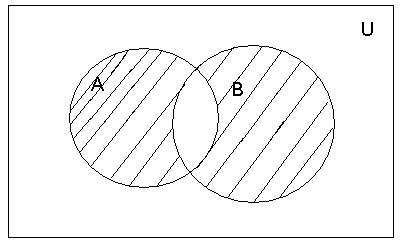
1. Объединением (суммой) множеств А и В называется множество С, состоящее из всех элементов множества А и всех элементов В (в том числе и тех, которые принадлежат А и В). Символически эту операцию можно записать так: АВ={хА хВ}, здесь -«или».

С=А+В=АВ, например А={1,2,3}; В={2,3,4}.

С= АВ={1,2,3,4}.

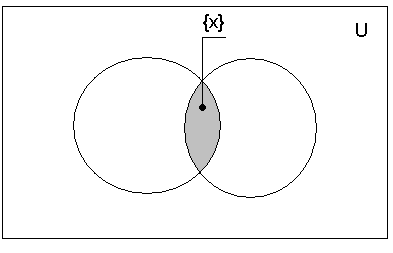
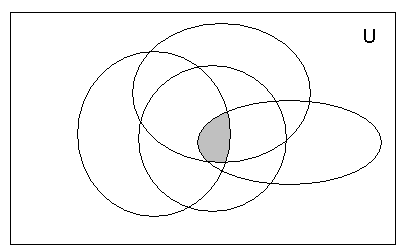
31)[2стр]2. Пересечением множеств А и В называется множество С, состоящее из элементов, входящих одновременно в А и В.

, здесь - операция «И»

если ,то . Например, , ,

Если Ǿ., то такие множества называются непересекающимися.

3. Разностью множеств А и В называется множество С, содержащее элементы множества А и не содержащее элементы множества В. ,например:

; ;

;

.

Если , то .

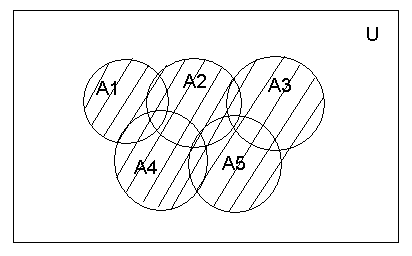
4. Симметрической разностью (дизъюнктивной суммой) называется множество С, элементы которого принадлежат либо А, либо В, но не обоим вместе (рис.5).

= . Например, ; ;

.

5. Абсолютным дополнением множества А до универсального множества называется множество, все элементы которого принадлежат и не принадлежат А.

. (рис.6). Очевидно, что .

Дополнение А определяется отрицанием свойства , с помощью которого определяется А.

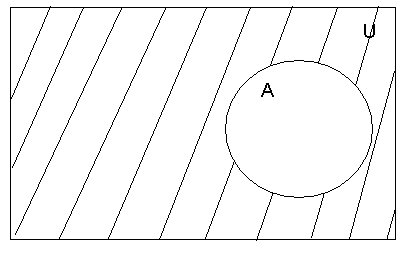
Рис.6.- Иллюстрация операции дополнение

32. Основные свойства алгебры множеств.

Операции над множествами обладают некоторыми свойствами, как и операции над числами, т.е. подчиняются следующим законам:

1. Коммутативный закон (переместительное свойство)

; .

;

2. Ассоциативный закон (сочетательное свойство).

; ;

;

3. Дистрибутивный закон (распределительное свойство)

;

;

4. Оригинальные операции:

5. Закон поглощения:

6. Теорема де Моргана:

,

7. ; ;

8. ;