Свойства коэффициента эксцесса

• .

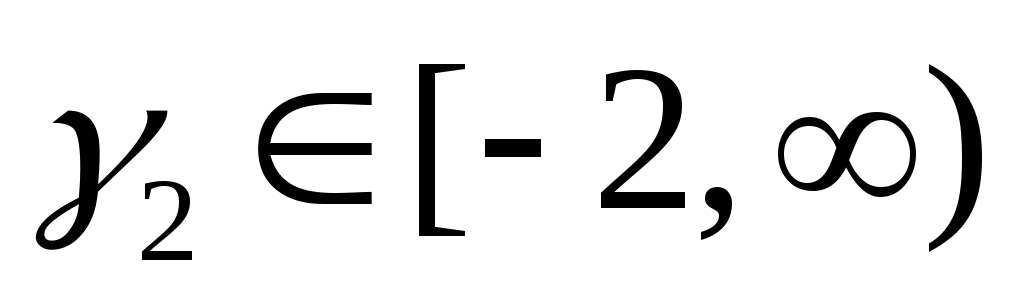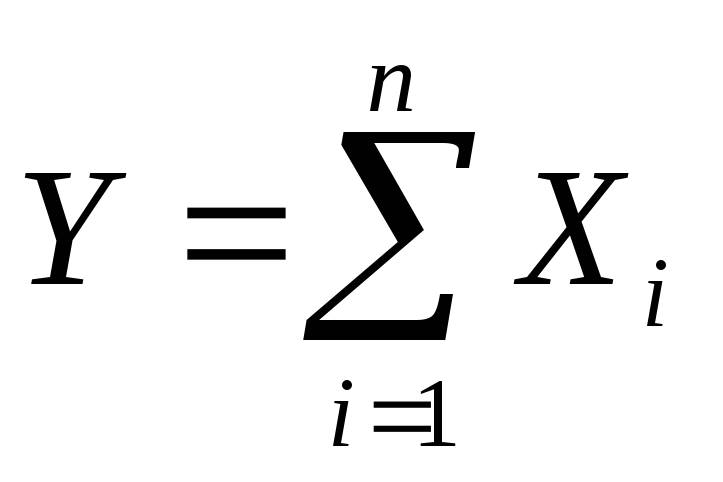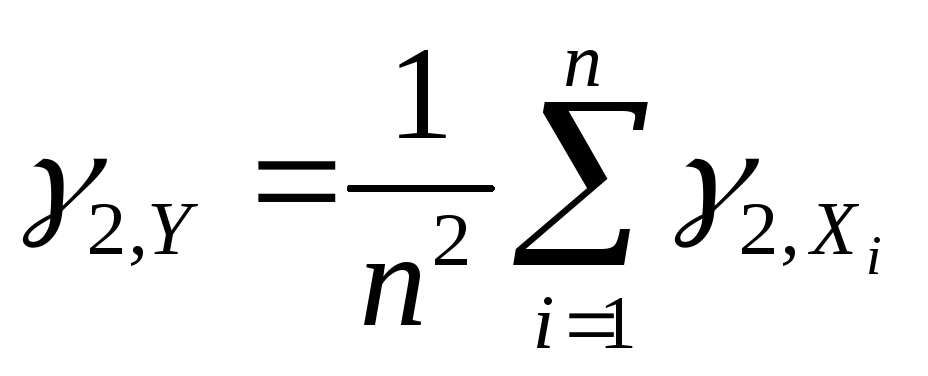• Пусть X₁,X₂,…,X_n— независимые случайные величины с равной дисперсией. Пусть. Тогда ,где 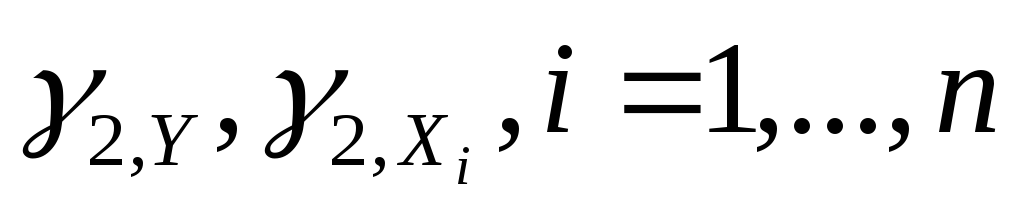— коэффициенты эксцесса соответствующих случайных величин.

Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет ее средний разброс.

Равен отношению стандартного отклонения к математическому ожиданию.

Так же используется такие обозначение:

Смысл коэффициента

В отличие от среднего квадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. Исчисляется в процентах. Вычисляется только для количественных данных.

 

50. Законы распределения дискретной случайной величины: биномиальное распределение. Параметры распределения. Математическое ожидание и дисперсия случайной величины, распределение по биномиальному закону.

Биномиа́льное распределе́ние в теории вероятностей— распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна P

Говорят, что с.в.Х имеет биномиальное распределение, если ее возможные значения равны 0,1,2…,к, …n, а соответствующие вероятности определяются по формуле (1). . Это название связано с тем, что равно коэффициенту при в разложении бинома

Возникает вопрос, какое максимальное значение принимает , если рассматривать , как функцию от k при фиксированном n? С этой целью рассмотрим отношение

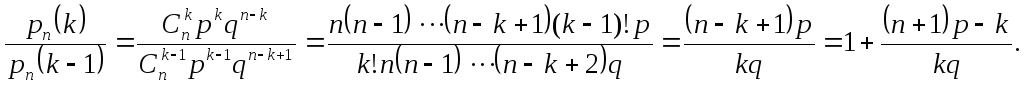
50)[стр2]Отсюда следует, что будет больше , если и меньше, если . Если - целое число, то Р_n (m)=Р_n (m-1). Это значит, что в двух точках достигается максимальное по k значение . Исключая эту ситуацию, имеем только одно целое число m, которое заключено в интервале

максимизирующее вероятность

Распределение (1) зависит от двух параметров : и .

Рассмотрим числовые характеристики с.в., распределенной по биномиальному закону.

Математическое ожидание числа появления события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:

Очевидно, что общее число Х появлений события А в n испытаниях складывается из числа появления события А в отдельных испытаниях. Поэтому если Х₁ число появлений события А в 1-м испытании, Х₂ число появлений события А во 2-ом, Х_n – в n-ом, то общее число появлений события А в n опытах будет равно:

Тогда , где

- математическое ожидание числа появления события А в i – ом опыте. Определим его

Математическое ожидание числа появлений события в одном испытании равно вероятности этого события. Тогда

.

Дисперсия биномиального распределения с параметрами и равна произведению . .

Доказательство. По формуле дисперсии ;

Поскольку Х₁, Х₂,…Х_n независимы, то можно записать.

Определим

;

; с вероятностью и :

; ;