45. Функция плотности распределения вероятности, ее свойства
Плотность вероятности, плотность распределения вероятностей случайной величины X, - функция p(x) такая, что
и при любых a<b
вероятность события a<x<b равна
.
Если p(x) непрерывна,
то при достаточно малых ∆x вероятность
неравенства x<X<x+∆x приближенно равна
p(x)•∆x (с точностью до малых более
высокого порядка). Функция распределения
F(x) случайной величины x, связана с
плотностью распределения соотношениями
и,
если F(x) дифференцируема
Смысл плотности
распределения вероятностей лучше понять
через элемент плотности
.
Его можно записать в виде
Это соотношение
утверждает, что элемент вероятности
есть вероятность того, что случайная
величина Х лежит в интервале между
и
.
Из определения плотности распределения
вероятностей следуют следующие ее
свойства:
;
;
.
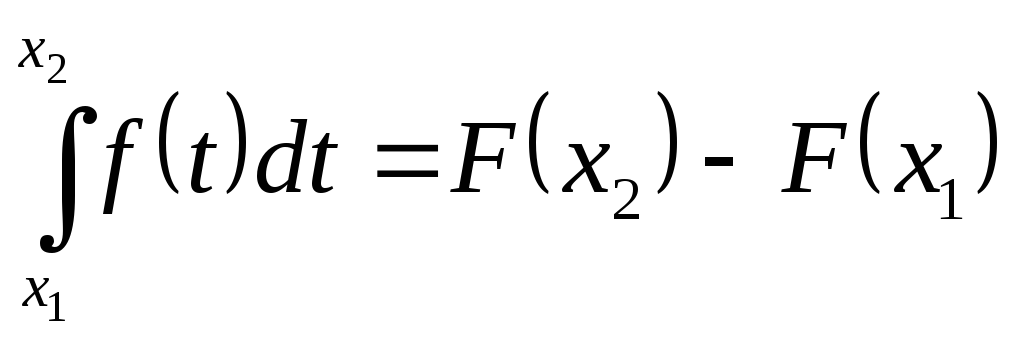Для дискретной случайной величины, производные в точках разрыва функции распределения не существуют. Однако плотность распределения такой случайной величины можно представить как совокупность d - функций разной интенсивности в точках разрыва функции распределения, т.е. таких d - функций, площадь каждой из которых (интеграл от d - функции) равняется соответствующему скачкообразному приращению функции распределения вероятностей.
46. Числовые характеристики случайных величин. Математическое ожидание дискретной и непрерывной случайной величины. Свойства математического ожидания
Среди числовых характеристик случайной величины прежде всего рассмотрим характеристики положения, фиксирующие положение свободной величины на числовой оси, к которым относятся математическое ожидание, мода и медиана.
Рассмотрим
дискретную случайную величину.
Пусть дискретная случайная величина X
принимает значения
и вероятность принятия случайной
величиной значения
равна
.
Интуитивно ясно, что при наблюдении
случайной величины X в n (n>>1) повторных
независимых экспериментах значение
появится примерно
раз. Таким образом, среднее значение
этой величины , подсчитанное по n
экспериментам , есть примерно
.
Поэтому математическим ожиданием или средним значением дискретной случайной величины X называется число
.
Если
и ряд
сходится абсолютно, математическим
ожиданием является величина
.
Основные свойства математического ожидания.
если
,
то
.
Математическое
ожидание постоянной величины равно
самой постоянной:
.
Постоянный множитель
можно выносить за знак математического
ожидания:
.
Действительно,
.
Математическое ожидание от суммы случайных величин X и Y равно
сумме математический ожиданий:
Свойства 2), 3) определяют линейность операции математического ожидания.
Если
,
то
Свойства 5), 6) очевидны.
Если случайные
величины X и Y независимы, то
С помощью введенной
плотности распределения вероятностей
легко получить математическое ожидание
для непрерывной случайной величины.
Действительно, разбив интервал изменения
случайной величины на маленькие
интервалы
и, так как приближенно
равно вероятности того, что случайная
величина Х примет значение
, то можно для непрерывной случайной
величины Х математическое ожидание
записать в виде
.
Правая часть этого
выражения представляет интегральную
сумму, поэтому, переходя к пределу
,
получаем
.