42. Понятие случайной величины. Классификация случайных величин. Примеры случайных величин.

Понятие случайной величины

Случайной величиной (с.в.) называется величина (число - вещественное или комплексное), которая в результате опыта может принять то, или иное значение (до проведения опыта неизвестное).С точки зрения инженерного подхода случайная величина - это просто числовое описание исходов случайного опыта. С точки зрения математики, случайная величина - это функция, которая определена на пространстве элементарных событий.

X = j(w), w Î W; x_i = j(w_i).

Различают два основных типа случайных величин: дискретные и непрерывные.

Дискретная случайная величина - это величина, множество возможных значений которой конечно или счетно.

Непрерывная случайная величина - это величина,. множество возможных значений которой континуально.

Разнообразие случайных величин весьма велико. Число принимаемых ими значений может быть конечным, счетным и несчетным; значения случайной величины могут быть расположены дискретно или заполнять интервалы сплошь.

Случайные величины будем обозначать заглавными буквами латинского алфавита (X, Y, Z,...), а их значения прописными буквами ( х, у, z,...).

Пример с.в.:

Поясним это на примере бросании игральной кости, где случайная величина Х - число выпавших очков. Из механики известно, что движение твердого тела полностью определяется, если заданы в некоторый момент шесть параметров, определяющих положение тела в пространстве, вместе со скоростями изменения этих параметров. Под элементарным событием w_i будем понимать набор этих двенадцати параметров в момент бросания. Тогда, зная w_i мы знаем и x_i, т.e. X есть функция w. Множество W, возможных значений w конечно, так как двенадцать параметров могут колебаться в конечных интервалах, а мы регистрируем их лишь с конечным числом десятичных знаков. Очевидно, что Х(w) наблюдать легко, в то время как при регистрации w_i возникают непреодолимые трудности. Кроме того, возможных значений w_i очень много, а значений Х(w_i) всего шесть. Отсюда видно, насколько сильно может быть упрощение математического описания явления при переходе от случайного события к случайной величине..

43. 3Акон распределения случайной величины. Закон распределения дискретной случайной величины.

Законом распределения с.в. называется всякое соотношение, устанавливающее связь между всеми возможными значениями с.в. и соответствующими вероятностями их появления.

Простейшим законом распределения является ряд распределения – одна из форм закона распределения дискретной с.в.

Закон распределения случайной величины Х или ряд распределения(закон дискр. с.в.), если заданы все значения случайной величины и вероятности появления этих значений, то есть

Х			…		…
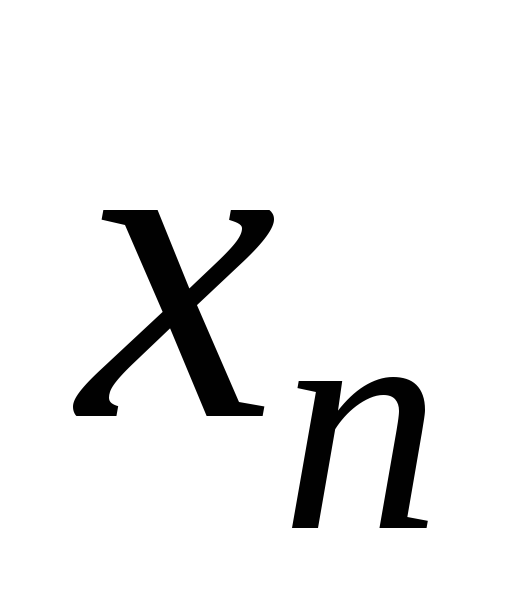
, р			…		…

где и .

Если задан ряд распределения случайной величины Х, то с вероятностной точки зрения дискретная случайная величина полностью описана. Так как события { X = x₁ }, { X = x₂ } несовместимы и образуют полную группу (это вытекает из определения. с.в.) то сумма всех вероятностей равна 1, т.е. . Эта единица (вероятность достоверного события, которым является пространство элементарных событий, каким то образом распределена между значениями с.в., отсюда и термин “распределение”.