35. Случайное событие. Классификация событий. Элементарное событие. Пространство элементарных событий.

События можно разделить на: достоверные, случайные и невозможные.

Достоверным событием называется такое событие, которое при выполнении комплекса условий обязательно произойдет. В дальнейшем будем его обозначать буквой .

Случайным событием называется такое событие, которое при выполнении комплекса условий может произойти, а может и нет. Будем его обозначать буквами А, В, С и т.д.

Невозможным событием называется такое событие, которое при выполнении комплекса условий никогда не произойдет. Будем обозначать его буквой О.

Реализация комплекса условий в котором наблюдается то или иное явление, называют опытом, (испытанием, эксперементом).

Каждому опыту (испытанию) соответствуют какие–то возможные исходы (результаты). Рассмотрим множество всех возможных исходов опыта и обозначим , каждый его элемент (один исход) будем называть элементарным событием и обозначать _i, а все множество – пространством элементарных событий.

Исходя из определения элементарные события обладают следующими свойствами :

1) наступление одного из них исключает другие исходы. (элементарные события)

2) одно из элементарных событий в результате опыте обязательно произойдет.

Любое событие А, наблюдаемое в опыте ,, можно рассматривать как подмножество , т.е. множество, состоящее из элементарных событий , в которых проявляется событие А , (А={₁, ₂, …, _m })

Определение: Элементарные события, входящие в подмножества, определяющие случайное событие, называются благоприятствующими данному событию.

Если множество благоприятствующих данному событию элементарных событий пусто, то такое событие называют невозможным и обозначают А= или А= U..

Если множество элементарных событий благоприятствующих данному событию совпадает с пространством элементарных событий , то такое событие называют достоверным и обозначают  или U. Иными словами, достоверное событие, это такое событие, которое реализуется при любом возможном исходе испытания.

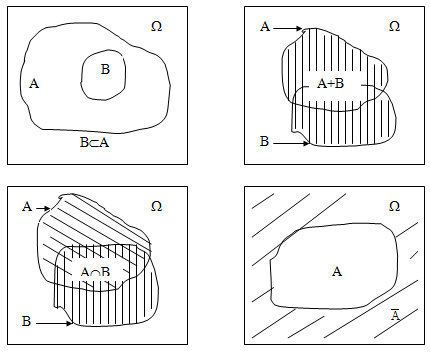
36. Случайное событие, как множество элементарных событий. Алгебра событий.

Так как события можно рассматривать как множества, состоящие из элементов (элементарных событий), то для них можно ввести операцию сложения (объединения) , умножения (пересечения) и дополнения.

Если А и В - два множества , то под их сложением (объединением), обозначаемым А+В (АВ), будем понимать множество состоящее из элементов (точек), входящих или в А, или в В:

А+В={_i: _iA или _iB}

Здесь А означает, что элемент  принадлежит множеству А.

На языке теории вероятностей А+В – событие , состоящее в том , что произошло хотя бы одно из событий А или В.

Под умножением (пресечением) множеств А и В , обозначаемым АВ (АВ), понимается множество , состоящее из элементов (точек), входящий и в А, и в В:

АВ={_i: _iA и _iB}.

В вероятностном смысле событие АВ состоит в том, что одновременно произошло и событие А, и событие В.

Если А – некоторое подмножество , то под его дополнением, обозначаемым , понимается множество элементов (точек) из , не входящих в А. Если В-А (В\А) – означает разность множеств (множество элементов В, не входящих в А), то =-А (\А) или А+=

На языке теории вероятностей означает событие противоположное событию А, т.е. событие, состоящее в ненаступлении события А.

Введем знак включения , который в теории множеств означает следующее. Пусть ВА, тогда В есть подмножество множества А. Другими словами множество В полностью состоит из элементов множества А. На языке событий это означает , что при появлении события В событие А обязательно произойдет.

Рассмотрим пример с двукратным бросанием монеты. Пусть А={ГГ, ГР, РГ} и В={ГР, РГ, РР} , то

А+В={ГГ, ГР, РГ, РР},

АВ={ГР, РГ},

={РР}.

Множества А и не имеет общих элементов, следовательно, множество А - пустое. Пустое множество будем обозначать О. Множество О в теории вероятностей, как было указано ранее, означает невозможное событие. С другой стороны А+= - достоверное событие.

События А и В называются несовместимыми , если их совместное событие невозможно . На языке множеств это означает , что АВ=0.

События В_i называются попарно несовместимыми, если В_iB_j=0 (ij, i,j=)

События В_i образуют полную группу событий, если

36)[стр2] В₁+ В₂+ …+В_N =.

Особый интерес представляют полные группы несовместимых событий

, т.е. =; В_iВ_j=; (ij, i,j=)

На приведенных ниже рисунках представлены диаграммы событий как множества, где геометрические точки означают элементарные события, а все точки квадрата образуют пространство элементарных событий .