5. Конечные автоматы, виды.

Конечный автомат — абстрактный автомат без выходного потока, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию.

Существуют различные варианты задания конечного автомата. Например, конечный автомат может быть задан с помощью пяти параметров: , где:

• Q — конечное множество состояний автомата;

• q₀ — начальное (стартовое) состояние автомата ();

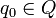• F — множество заключительных (или допускающих) состояний, таких что ;

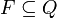• Σ — допустимый входной алфавит (конечное множество допустимых входных символов), из которого формируются строки, считываемые автоматом;

• δ — заданное отображение множества 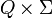во множество 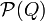подмножеств Q:

(иногда δ называют функцией переходов автомата).

Автомат начинает работу в состоянии q₀, считывая по одному символу входной строки. Считанный символ переводит автомат в новое состояние из Q в соответствии с функцией переходов. Если по завершении считывания входного слова (цепочки символов) автомат оказывается в одном из допускающих состояний, то слово «принимается» автоматом. В этом случае говорят, что оно принадлежит языку данного автомата. В противном случае слово «отвергается».

Конечные автоматы подразделяются на детерминированные и недетерминированные.

Детерминированным конечным автоматом (ДКА) называется такой автомат, в котором для каждой последовательности входных символов существует лишь одно состояние, в которое автомат может перейти из текущего.

Недетерминированный конечный автомат (НКА) является обобщением детерминированного.

Конечные автоматы широко используются на практике, например в синтаксических, лексических анализаторах, и тестировании программного обеспечения на основе моделей.

5. Построение дка на основе нка.

Алгоритм систем подмножеств

Смысл алгоритма состоит в замене множества из состояний НКА, множеством из подмножеств его состояний.

Алгоритм

Генерируем все подмножества множества состояний НКА — это состояния ДКА. Далее для всевозможных — пар состояний ДКА и символов , добавляем переход из в по , если для каждого состояния НКА из есть переход по в состояние из и, наоборот, в каждое состояние НКА из есть переход из состояния из по

Алгоритм Томпсона

Данный алгоритм используется для преобразования НКА в ДКА. Смысл этого алгоритма, как и предыдущего, состоит в замене множества из состояний НКА, множеством из подмножеств его состояний. Но не все из состояний будут присутствовать в ДКА, ввиду недостижимости многих из них, поэтому в алгоритме используется обход в ширину.

Алгоритм

Вначале в очередь помещается множество состоящее только из стартового состояния НКА . Затем из очереди изымается очередное множество — новое состояние ДКА. Если в есть допускающие состояния, то оно допускающее. Функция перехода строится по следующему правилу: . В результате задаст новое состояние автомата. Если еще нет в ДКА, тогда мы помещаем в очередь. Так как - конечна, а , то алгоритм завершится за конечное число шагов. Отсюда же получается верхняя оценка на время работы алгоритма — в худшем случае это .