48. Вычисление тройного интеграла в декартовых координатах.
(25.1)
где v – объем области V.
Вычисление тройных интегралов в декартовых координатах основано на понятии правильной пространственной области. Область V называют правильной в направлении оси Oz, если:
1) всякая прямая, проходящая через внутреннюю точку пространственной области V параллельно оси Oz, пересекает только один раз (только одну) «поверхность входа» и только один раз (только одну) «поверхность выхода»;
2) проекция D пространственной области V на плоскость xOy является правильной плоской областью в направлении оси Ox или Oy.
Пусть область V
является правильной в направлении оси
Oz,
ограниченной снизу поверхностью
а сверху – поверхностью
(рис. 25.1). Пусть она проектируется на
область
элементарную в направлении оси Oy,
и снизу ее ограничивает кривая
а сверху – кривая
(рис. 25.2).
|
Рис. 25.1 |
Рис. 25.2 |
Тогда справедлива следующая формула:
(25.2)
причем интеграл
в правой части равенства называется
повторным
интегралом
от функции f(x; y; z)
по области V
с внешним интегрированием по x,
а
– внутренним
интегралом
по переменной z.
Аналогично рассматривают пространственные области, правильные в направлении оси Ox или Oy, и применяют соответствующие формулы перехода к повторным интегралам.
Если область интегрирования V не подпадает под эти случаи, необходимо произвести разбиение этой области V на конечное число правильных областей и воспользоваться свойством аддитивности.
49. Вычисление тройного интеграла в цилиндрических координатах.
Если область интегрирования при вычислении тройного интеграла представляет собой тело, ограниченное цилиндром или некоторой его частью, целесообразно перейти к цилиндрическим координатам.
Формулы перехода
от декартовых координат x,
y
и z
к цилиндрическим координатам
и z
имеют вид:
(25.3)
где
(или
),
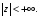Формула
замены переменных в тройном интеграле
при переходе к цилиндрическим координатам
имеет вид:
(25.4)где
– область в цилиндрической системе
координат,
соответствующая
области V
в декартовой системе координат;f(x; y; z)
– функция, непрерывная в этой области.
Вычисление тройных интегралов в
цилиндрических координатах
основано на понятии правильной
пространственной области.Область
V
называют правильной пространственной
областью в направлении оси Oz
в цилиндрической системе координат,
если:1) переход от декартовых координат
к цилиндрическим осуществляется по
формулам (25.3);2) всякая прямая, проходящая
через внутреннюю точку пространственной
области V
параллельно оси Oz,
пересекает только один раз (только одну)
«поверхность входа» и только один раз
(только одну) «поверхность выхода»;3) проекция
D
пространственной области V
на плоскость хОу
является правильной в полярной системе
координат.Аналогично в случае перехода
к цилиндрическим координатам по формулам
или
вводят понятие правильной пространственной области в направлении оси Оу или оси Ох в цилиндрической системе координат.