7. Интегрирование иррациональных функций. Первая подстановка Эйлера.

R(u₁,…,u_n) =

Допустим, что в свою очередь переменные u₁, …, u_n – сами являются функциями: u_1­ = f₁(x), …, u_n­ = f_n(x). Тогда ф-я R(f₁(x),…, f_n(x)) называется рациональной ф-ей от функций f₁(x),…, f_n(x).

Рассмотрим случай, когда интегрирование иррациональных ф-й можно свести с помощью некоторой подстановки к интегралу рациональных ф-й.

Этот интеграл сводится к интегрированию от рациональных

ф-й другой переменной следующей подстановкой:

1-я подстановка Эйлера а>0

- Будет одинаково

Затем подставляем под интеграл.

8. Интегрирование иррациональных функций. Вторая подстановка Эйлера.

R(u₁,…,u_n) =

Допустим, что в свою очередь переменные u₁, …, u_n – сами являются функциями: u_1­ = f₁(x), …, u_n­ = f_n(x). Тогда ф-я R(f₁(x),…, f_n(x)) называется рациональной ф-ей от функций f₁(x),…, f_n(x).

Рассмотрим случай, когда интегрирование иррациональных ф-й можно свести с помощью некоторой подстановки к интегралу рациональных ф-й.

Этот интеграл сводится к интегрированию от рациональных

ф-й другой переменной следующей подстановкой:

2-я подстановка Эйлера

Пусть имеет различные действительные корни x₁ и x₂. В этом случае применяют 2-ю подстановку Эйлера:

=

9. Определенный интеграл. Определение. Физический и геометрический смысл.

Пусть ф-я f(x) определена на отрезке [a,b]. Разобьем его на n-частей и составим интегральные суммы.

Число I называется пределом интегральных сумм:

ф-ии f(x) на отрезке [a,b], если для любого ε > 0 существует δ>0, что для любого разбиения отрезка [a,b] на части с длинами < δ, неравенство:

выполняются при любом выборе точек .

Если при любом разбиении отрезка [a,b] на части и при любом выборе точек на их интегральные суммы имеют один и тот же конечный предел, то этот предел называется определенным интегралом и обозначается:

Геометрический смысл определенного интеграла: определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

Физический смысл определенного интеграла: пусть материальная точка M движется вдоль числовой оси со скоростью V(t), Тогда путь, пройденный точкой за промежуток времени от до равен определенному интегралу от скорости:

10. Свойства определенного интеграла. Теорема о среднем.

1)

2)

3)

равенства 2 и 3 в совокупности называются свойством линейности;

4)

5)

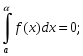
6) значение интеграла не зависит от обозначения переменной интегрирования:

7) свойство аддитивности: при любом взаимном расположении чисел a, b, c имеет место формула:

8) если при то

9) если m и M – соответственно наименьшее и наибольшее значения функции на отрезке [a; b], то верна оценка

10)

11) если функция f (x) непрерывна на отрезке [a; b], то существует точка такая, что

12) если f (x) – нечетная функция, то

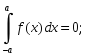
13) если f (x) – четная функция, то

14) если f (x) – периодическая функция периода T, то при любом верно равенство

Теорема о среднем(без доказательства!!!):

Пусть ф-я f(x) неопр. На [a,b] тогда на этом отрезке найдется по крайней мере одна точка такая что имеет место равенство: