53. Формула Грина.

Формула Грина: если функции P(x; y) и Q(x; y) непрерывно дифференцируемы в замкнутой ограниченной области D, то имеет место формула Грина:

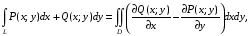(26.10)

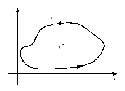
где L – граница области D, интегрирование вдоль которой производится в положительном направлении (рис. 26.2).

54. Поток вектора через поверхность. Его свойства.

Поток векторного поля через поверхность — поверхностный интеграл первого рода по поверхности S. По определению

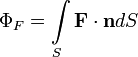
Где векторное поле (вектор-функция векторного аргумента — точки пространства), n - единичный вектор положительной нормали к поверхности (положительное направление выбирается для ориентируемой поверхности условно, но одинаково для всех точек — то есть для дифференцируемой поверхности — так, чтобы n- было непрерывно; для неориентируемой поверхности это не важно, так как поток через неё всегда ноль), dS — элемент поверхности.

В трёхмерном случае

а поверхностью является обычная двумерная поверхность.

Иногда, особенно в физике, применяется обозначение

тогда поток записывается в виде

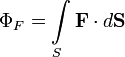
55. Поток вектора через незамкнутую поверхность

56. Поток вектора через замкнутую поверхность. Теорема Гауса-Остроградского.

Фо́рмула Острогра́дского — формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью: 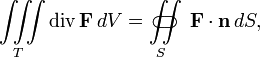то есть интеграл от дивергенции векторного поля , распространённый по некоторому объёму T, равен потоку вектора через поверхность S, ограничивающую данный объём. то есть интеграл от дивергенции векторного поля , распространённый по некоторому объёму T, равен потоку вектора через поверхность S, ограничивающую данный объём. Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.

В работе Остроградского формула записана в следующем виде:v 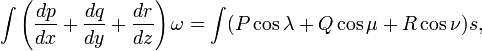где ω и s — дифференциалы объёма и поверхности соответственно. В современной записи ω = dΩ — элемент объёма, s = dS — элемент поверхности.

функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.

Обобщением формулы Остроградского является формула Стокса для многообразий с краем.Фо́рмула Острогра́дского — формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:

57. Дивергенция векторного поля.

дивергенция — это дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.

Оператор дивергенции, применённый к полю F oбозначают как div F

Определение дивергенции выглядит так:

где ФF — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся к нулю 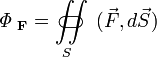Это определение, в отличие от приводимого ниже, не привязано к определённым координатам, например, к декартовым, что может представлять дополнительное удобство в определённых случаях. (Например, если выбирать окрестность в форме куба или параллелепипеда, легко получаются формулы для декартовых координат, приведённые в следующем параграфе).