45. Еквівалентні схеми пасивних чотириполюсників

Пасивний 4-пол, у якого опори елементів схеми сталі, можна звести до однієї з еквівалентних схем заміщення з трьома вітками, з'єднаними зіркою або трикутником.

Т-подібна схема заміщення: Три вітки пасивного 4-пол, з'єднані зіркою, утворюють Т-подібну схему заміщення (рис. 18.5, а). Для цієї схеми струм на вході

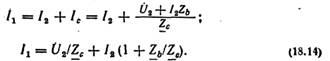
Н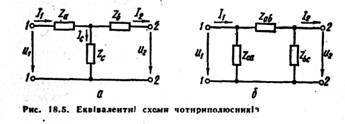апруга на вході Підставивши Іг (І1), дістанемо

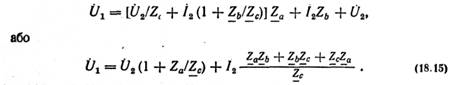
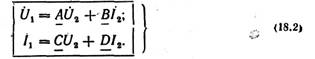
Зіставивши добуті рівняння вхідних значень струму і напруги з рівняннями 4-пол (18.2), знайдемо вирази коефіцієнтів Т-подібної схеми заміщення пасивного 4-пол:

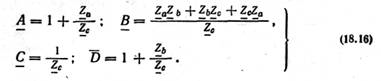
П-подібна схема заміщення

В схемі (рис. 18.5, а) зірку опорів Za, Zb, Zc можна замінити Після такої заміни дістанемо еквівалентну П-подібну схему заміщення пасивного 4-пол (рис. 18.5, б). Виразимо вхідні величини цієї схеми: 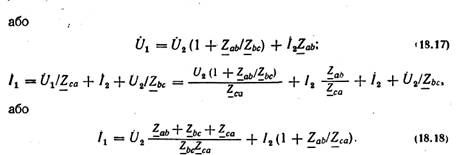Зіставивши добуті рівняння напруги (18.17) і струму (18.18) з основними рівняннями 4-пол (18.2), знайдемо вирази коефіцієнтів для П-подібної схеми заміщення пасивного 4-пол: 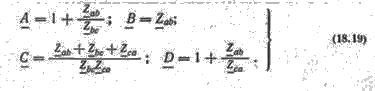Зведення будь-якої схеми 4-пол до однієї з еквівалентних схем

Параметри схем заміщення й сталі пасивного 4-пол пов'язані формулами (18.16) і (18.19). З них неважко виразити опори Т- і П-подібних схем.

Параметри: Т-подібної схеми з (18.16)

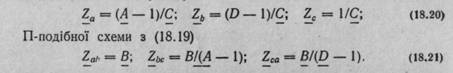
Звідси випливає спосіб зведення будь-якої заданої схеми пасивного 4-пол до однієї з еквівалентних схем:

1. Визначити розрахунок або на підставі досліду коефіцієнти А, В, С, D заданого 4-пол.

2. За формулами (18.20) або (18.21) знайти параметри еквівалентної схеми заміщення.

Далі еквівалентну схему можна використати для аналізу заданого 4-пол поряд з вихідною схемою.

46. Еквівалентні схеми активних неавтономних 4-пол

41. Еквівалентна схема приведеного трансформатора і його векторна діаграма

(Загалом параметри первинної обмотки трансформатора відрізняються від параметрів вторинної обмотки. Різниця найбільш відчутна при великих коефіцієнтах трансформації. Труднощі в розрахунках можна усунути, якщо привести всі параметри трансформатора до однакового числа витків, наприклад, до w 1. З цією метою параметри вторинної обмотки перераховуються на число витків w 1.)

Замість реального трансформатора з коефіцієнтом трансформації k = w 1/w 2, отримують еквівалентний трансформатор з k = w 1/w 2 = 1. Такий трансформатор називається приведеним.

(При приведенні всі потужності і фази вторинної обмотки повинні залишитися такими ж, що і в реальному трансформаторі.

Наприклад, якщо повна потужність вторинної обмотки реального трансформатора S 2 = E 2 I 2, то вона повинна дорівнювати повній потужності вторинної обмотки наведеного трансформатора: Використовуючи раніше отриманий вираз I 2 '= I 2 w 2 / w 1, напишемо вираз для E 2': .

Прирівняємо тепер активні потужності вторинної обмотки:

Визначимо наведений активний опір:

за аналогією: )

Рівняння ЕРС і струмів для наведеного трансформатора тепер будуть мати вигляд:

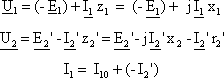
Побудова векторної діаграми трансформатора

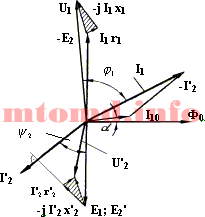
Побудова векторної діаграми зручніше починати з вектора основного потоку Ф. Відкладемо його по осі абсцис. Вектор I 10 випереджає його на кут a. Далі будуємо вектори ЕРС Е 1 та Е 2 ', які відстають від потоку Ф на 90 °. Для визначення кута зсуву фаз між E 2 'і I 2' слід знати характер навантаження. Припустимо, вона активно-індуктивна. Тоді I 2 'відстає від E2' на кут f 2.

Вийшла так звана заготівля векторної діаграми трансформатора (малюнок). Для того щоб добудувати її, необхідно скористатися трьома основними рівняннями наведеного трансформатора .

Скористаємося другим основним рівнянням і зробимо додавання векторів:

(Для цього до кінця вектора E 2' прилаштуємо вектор - j I 2' x 2 ', а до його кінця - вектор - I 2' r 2 '. Результуючим вектором U 2' буде вектор, що з'єднує початок координат з кінцем останнього вектора. Тепер використовуючи третій основне рівняння: з якого видно, що вектор струму I 1 складається з геометричної суми векторів I 10 і - I 2 '. Зробимо це підсумовування і добудуємо векторну діаграму трансформатора . Тепер повернемося до першого основного рівняння: Щоб побудувати вектор - Е 1, потрібно взяти вектор + Е 1 і направити його в протилежну сторону. Тепер можна складати з ним і інші вектори: + j I 1 x 1 і I 1 r 1. Перший буде йти перпендикулярно струму, а другий - паралельно йому. В результаті отримаємо сумарний вектор u 1.)

Еквівалентна схема трансформатора. Схема заміщення трансформатора. Т-подібна схема заміщення трансформатора.

Рисунок 1 - Схема наведеного трансформатора Рисунок 2 - Т-подібна схема заміщення трансформатора

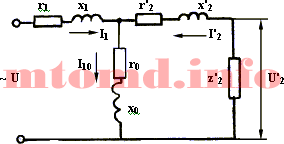
На (рис.1) представлена ​​еквівалентна схема наведеного трансформатора , на якій опору r і x умовно винесені з відповідних обмоток та включені з ними послідовно. Так як k = 1, то E 1 = E 2. Тому точки А і а, а також Х і х на наведеному трансформаторі мають однакові потенціали, що дозволить електрично з'єднати ці точки, отримавши Т-подібну еквівалентну схему заміщення (рис.2). Провівши математичний опис цієї схеми методами Кірхгофа, можна зробити висновок про те, що вона повністю відповідає рівнянням ЕРС і струмів реального трансформатора