34.Синтез реактивних двополюсників.

Параметри індуктивно-зв’язаних елементів. Коефіцієнт магнітного зв’язку. Однойменні полюси індуктивно-зв’язаних елементів. Сутність явища взаємної індукції полягає у виникненні ЕРС в якій-небудь котушці (контурі) внаслідок зміни струму в іншій котушці (контурі). Це явище відображає взаємний зв’язок котушок, зчеплених із загальним магнітним потоком. Кола, в яких наводяться ЕРС взаємної індукції, називають колами з індуктивно зв’язаними вітками. Повна ЕРС, індукована у першій котушці: 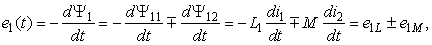(12.3)

у другій котушці: 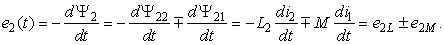(12.3)

ЕРС взаємної індукції враховують у виразах (12.7), (12.8) з додатним знаком “” у разі узгодженого ввімкнення котушок, та зі знаком „” у разі зустрічного увімкнення котушок.

Кількісною характеристикою явища взаємоіндукції є не тільки взаємна індуктивність , а також і коефіцієнт зв’язку індуктивно зв’язаних котушок, який показує, яка частина потоків самоіндукції двох індуктивно зв’язаних котушок є одночасно потоком взаємоіндукції: 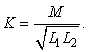(12.9)

ПРИКЛАД 12.2.

Коефіцієнт зв’язку завжди менший за одиницю. Доведемо це, склавши вираз для :

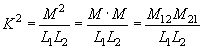
Підставимо у співвідношення (12.10) вирази для взаємних індуктивностей (із 12.1) та індуктивностей котушок.

Якщо

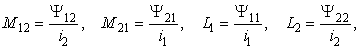
тоді

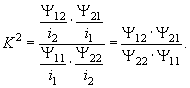
Оскільки потокозчеплення взаємоіндукції – це частини потоків самоіндукції (), то . Лише в ідеальному випадку, коли обидві котушки суміщені і кожний з потоків самоіндукції повністю (без розсіювання) зчеплюється з іншою котушкою () коефіцієнт зв’язку дорівнює одиниці Такий ідеальний зв’язок називають абсолютним.

Індуктивний зв’язок між котушками можна змінювати, якщо переміщувати одну котушку відносно іншої. Прилади, які складаються з двох котушок, що взаємно переміщуються, називають варіометрами.

Зміна струму в одному із індуктивно зв’язаних елементів спричинює виникнення ЕРС взаємної індукції в іншому (12.4), (12.6); при цьому між його затискачами з’являється напруга. В процесі розрахунків кіл синусоїдного струму, які містять індуктивно зв’язані котушки, необхідно з відповідним знаком враховувати ЕРС взаємної індукції , що наводяться в цих котушках. Знак ЕРС взаємної індукції у виразах для повної індукованої ЕРС (12.7), (12.8) залежить від способу увімкнення котушок (узгоджено, зустрічно). На схемах інформацію про спосіб зв’язку подають за допомогою спеціального маркування затискачів індуктивно зв’язаних котушок.

Два затискача, що належать двом різним індуктивно зв’язаним елементам кола, називають однойменними і позначають однаковими значками, керуючись таким правилом: за однакового напрямку струмів відносно однойменних затискачів магнітні потоки самоіндукції і взаємної індукції у кожному елементі повинні додаватися.

Однойменні затискачі котушок легко визначити, якщо відомі напрямки намотування витків котушок і обрані додатні напрями струмів через котушки (рис.12. 2).

Р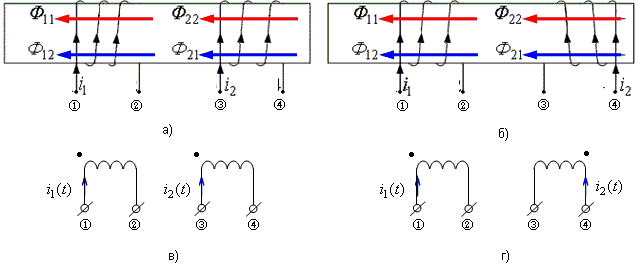ис. 12.2. Маркування однойменних затискачів узгоджено увімкнених котушок: фізична реалізація (а), (б), позначення на схемах (в) (г)

На рис. 12.2,а) однойменними є затискачі – та – ; на рис. 12.2,б) однойменні затискачі – це – та – . Для розмітки затискачів треба скористуватися правилом, наведеним вище. Наприклад, для котушок, зображених на рис. 12,а), вочевидь, при спрямуванні струму від затискача до затискача та струму від затискача до затискача магнітні потоки самоіндукції () і взаємної індукції () спрямовані однаково і додаються. Тому затискач є однойменним до затискача , а – до .

Щоб спростити креслення на схемах, зазвичай осердя котушок не зображають, а одну із пар однойменних затискачів позначають спеціальними значками: крапками (рис. 12. 2,в),г)), зірочками, трикутниками і т. і. У тих випадках, коли встановити взаємне розміщення котушок і напрямок намотування їх витків складно, для визначення однойменних затискачів можна здійснити дослід (рис. 12.3).

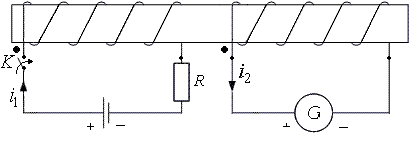Рис. 12.3. Схема досліду для визначення однойменних затискачів індуктивно зв’язаних котушок

Одна з котушок з’єднується з гальванометром, а інша підключається до гальванічного елементу (рис. 12.3). При вмиканні ключа виникає короткочасний струм , який послаблює магнітне поле, створене струмом . Отже, в момент вмикання джерела живлення струми і спрямовані протилежно відносно однойменних затискачів. Напрямок струму визначається полярністю джерела живлення. Про напрям струму роблять висновок, аналізуючи короткочасне відхилення стрілки гальванометра. Якщо стрілка відхиляється у бік шкали, то струм спрямований до додатного затискача гальванометра. У такому разі затискачі обох котушок, які приєднані до додатних затискачів гальванометра і джерела живлення, є однойменними.

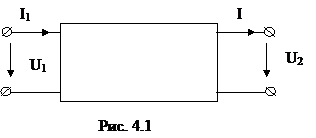
43.

Чотириполюсником називають електричний ланцюг (рис.4.1), в якій важливими є дві гілки, одна з яких вхідна, а інша - вихідна Будемо вважати визначальними величинами: U1, I1, U2, I2 Поставимо мета, вважаючи відомими будь-які дві з перерахованих величин, знайти дві залишилися. Таких варіантів буде шість. Вони визначають наступні форми запису рівнянь чотириполюсників:

форма Y

форма Z

форма B

форма A

форма H

форма F

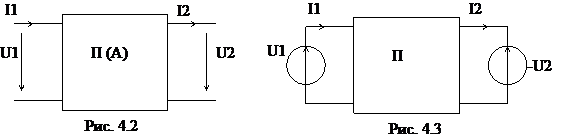
Здійснимо висновок рівнянь пасивного чотириполюсника в Y-формі. Скористаємося методом накладання. Розглянемо чотириполюсник (рис. 4.2), і виконаємо висновок рівнянь пасивного чотириполюсника. Для цього чотириполюсник представимо у вигляді рис. 4.3, де вхідний і вихідний напруги замінені фіктивними джерелами.

За принципом незалежності дії джерел струм в кожній гілці можна визначити, підсумовуючи складові струмів від кожного джерела ланцюга. Схема (рис. 4.3) буде еквівалентна сукупності двох схем (рис. 4.4 і.4.5).

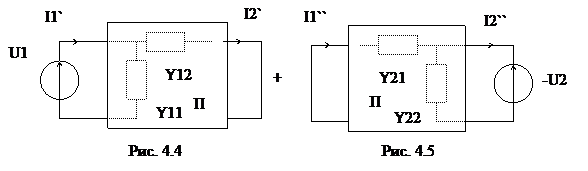
Визначимо струми i1’ и i2’ за законом Ома

де Y11 Вхідна провідність; Y12 Вхідна провідність між входом і виходом.

За аналогією:

де Y12 вихідна провідність; Y12=Y21 Відповідно до методу накладення маємо

Останні рівняння є Y-форму запису рівнянь чотириполюсника. Виведемо рівняння пасивного чотириполюсника в Z-формі. Для виведення скористаємося рівняннями Y-форми:

Введемо матрицю: , Обчислимо визначники:

Тоді вхідний і вихідний напруги рівні:

або після формування стовпців струмів:

Якщо ввести матриці-стовпчики напруг і струмів, то можна отримати рівняння в матричному вигляді. Введемо

матриці-стовпці , Тоді рівняння в матричному вигляді візьмуть вид в Y-формі:

і в Z-формі:

Якщо позначити коефіцієнти в правих частинах останніх рівнянь опорами, то рівняння Z-форми приймуть вид:

З цієї системи висловимо

Звідки видно, що

Виведемо рівняння пасивного чотириполюсника в А-форме. При виведенні також скористаємося рівняннями Y-форми:

З першого рівняння отримаємо:

Ця напруга підставимо в друге рівняння і знайдемо струм:

Система рівнянь прийме вигляд А-форми:

Якщо в рівняннях поміняти місцями індекси та коефіцієнти А і D, то можна отримати рівняння В-форми:

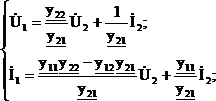АБО

Особлива властивість коефіцієнтів у рівняннях А-форми (перевірка розрахунків) полягає в тому, що різниця творів коефіцієнтів A, D і B, C дорівнює одиниці:

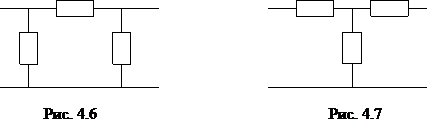
AD - BC = 1. Звідси випливає: будь пасивний чотириполюсник можна уявити трьохелементної схемою (рис. 4.6, 4.7). Поступаючи аналогічно, можна отримати рівняння Z-, H-, F-форм.

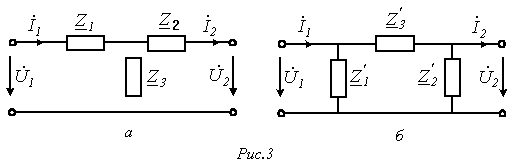
44. При визначенні коефіцієнтів чотириполюсника розрахунковим шляхом повинні бути відомі схема з'єднання і величини опорів чотириполюсника. Пасивний чотириполюсник характеризується трьома незалежними постійними коефіцієнтами. Отже, пасивний чотириполюсник можна представити у вигляді трьохелементної еквівалентної Т - (рис. 3, а) або П-образної (рис. 3, б) схеми заміщення. . Для визначення коефіцієнтів отириполюсника для схеми на рис. 3, а з використанням першого і другого законів Кірхгофа висловимо и і через через и і : :

; ;

(9) (9)

. .

(10) (10)

Зіставлення отриманих виразів (9) і (10) з співвідношеннями (3) і (4) дає:

Дане завдання може бути вирішена і іншим шляхом. При (Холостий хід з боку вторинних затискачів) відповідно до (3) і (4) и і ; ;

але зі схеми на рис. 3,а

, а , А ; ;

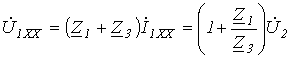звідки випливає: и і . .

При (Коротке замикання на вторинних затискачах)

и і . .

Зі схеми на рис. 3, а

; ;

. .

Отже, . .

Таким чином, отримані ті ж самі результати, що і в першому випадку. Коефіцієнти чотириполюсника для схеми на рис. 3,б можуть бути визначені аналогічно або на підставі отриманих для ланцюга, а з використанням розглянутих раніше формул перетворення "зірка-трикутник". З вищесказаного можна зробити висновок, що знаючи коефіцієнти чотириполюсника, завжди можна знайти параметри Т-і П-подібних схем його заміщення. а практиці часто виникає потреба в переході від однієї форми запису рівнянь чотириполюсника до іншої. Для вирішення цього завдання, тобто щоб визначити коефіцієнти однієї форми запису рівнянь через коефіцієнти інший, слід висловити будь-які дві однакові величини в цих формулах через дві інші і зіставити їх з урахуванням позитивних напрямків струмів для кожної з цих форм. Так при переході від А-до Z-формі на підставі (4) маємо

. .

(11) (11)

Підстановка співвідношення (11) в (3) дає

. .

(12) (12)

Зіставляючи виразу (11) і (12) з рівняннями чотириполюсника в Z-формі (див. табл. 1), отримаємо

. .

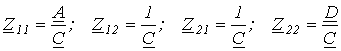При аналізі роботи чотириполюсника на навантаження зручно використовувати поняття вхідного опору з первинної сторони і коефіцієнта передачі . Враховуючи, що и і 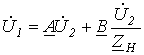, Для цих параметрів можна записати:

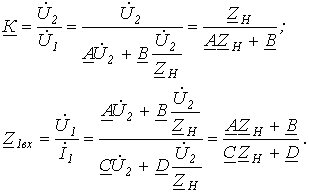
Знаючи , , и і , Можна визначити інші змінні на вході і виході чотириполюсника: ; ; ; ;
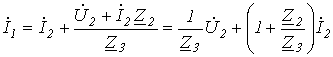
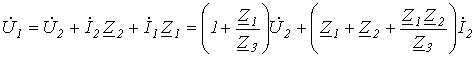
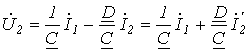
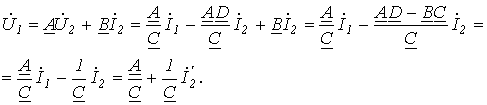