Матричные преобразования объектов Двумерные преобразования относительно координат.

1. Сдвиг.

y

Сдвиг точки по OY обозначается D_y,

P’(x’,y’) по OX обозначается D_x,

D_y x’ = x + D_x,

P(x,y) y’ = y + D_y,

Важен знак коэффициента D.

x

D_x

[x’, y’] = [x, y] + [D_x, D_y]

P’ = P + T

Теоретически для любого изображения нужно выполнить такие действия над каждой точкой изображения. Если имеем дело с векторным изображением, то для отрезка (А, В) достаточно выполнить перенос концов отрезка (А’, В’). Данное утверждение справедливо для действий масштабирования и поворота. Три действия сдвиг, масштаб и поворот позволяют получить абсолютно любое пространственное преобразование объекта.

2. Масштабирование.

y

P’(x’, y’)

P(x,y)

x

При масштабировании координаты точки умножаются на коэффициент масштабирования.

x’ = x * S_x

y’ = y * S_y

Запишем в матричной форме коэффициент масштабирования S.

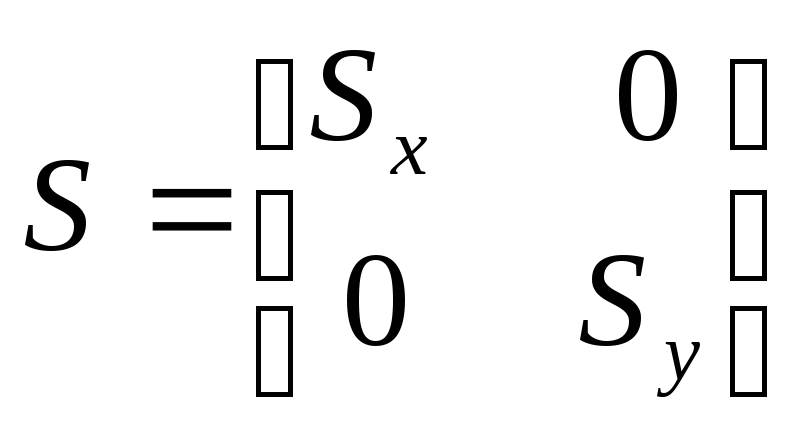
Тогда

P’ = P * S

Для пиксельных изображений такое преобразование нужно выполнить над каждой точкой, для векторного над концами каждого отрезка.

Для простоты промасштабируем по обоим осям.

Пример. Пусть начало отрезка проходит через начало координат.

1) y

Промасштабируем его по обеим осям с коэффициентом 2.

P₂(1,1) S_x = S_y = 2.

P₃(0.5;0.5)

x

P₁(0,0)

Тогда получится

y

P₂‘(2, 2)

P₁‘(0,0)

2) Возьмём P₃(0.5;0.5). Выполним масштаб по обеим осям с тем же коэффициентом. Зрительно отрезок как бы сместился вправо. При масштабировании это происходит всегда.

y

P₂(2,2)

P₃(1,1)

x

3. Поворот. Если известен угол поворота , то

y

P₂‘(x’,y’) x’ = x cos  – y sin 

y’ = x sin  + y cos 

 P(x,y)

x

В матричной форме

Или P’ = P * R, где R – это матрица поворота. При движении против часовой стрелки угол поворота считается положительным, при движении по часовой стрелке угол поворота отрицательный. Недостатки в преобразованиях: сдвиг выполняется через сложение, а масштаб и поворот через умножение. При достаточно сложном объекте это неудобно. Чтобы уйти от сложения в сдвиге объекта, из математики позаимствовали понятие однородных координат.

P(W_x,W_y,W)

То есть, для точки в двухмерном пространстве появляется фиктивная третья координата:

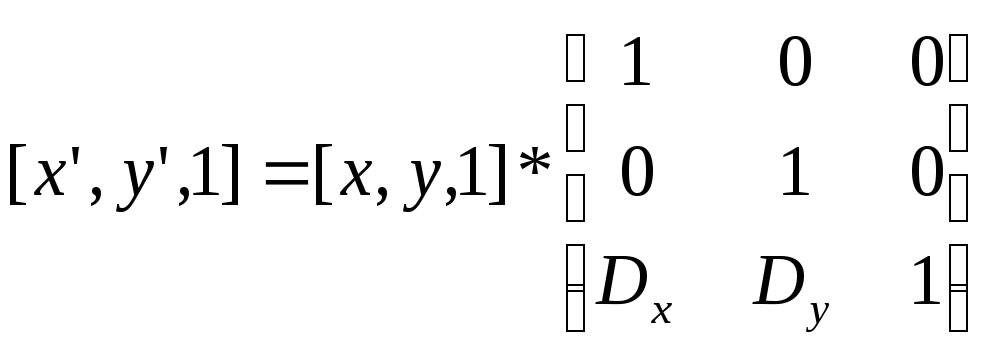
Тогда сдвиг выполняется в матричной форме через умножение P’ = P * T. Таким же образом третья координата добавляется в действие масштабирования и поворота.

Для масштабирования:

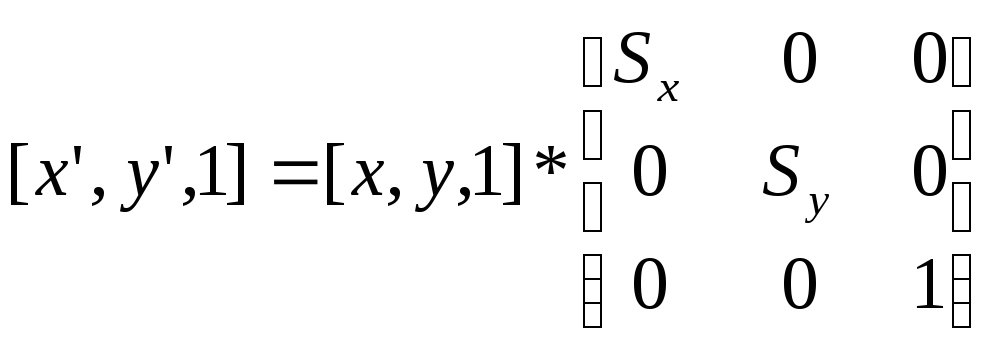
Для поворота:

P’ = P * T * S *R – даёт наименьшее количество операций умножения.

Двухмерное преобразование относительно произвольной точки.

P(x,y) – над которой выполняется преобразование

P₁(x₁,y₁)

Результирующее положение точки P’(x’,y’). Относительно начала координат мы знаем. Проще всего так:

1. Сдвинем начало координат в точку P₁(x₁,y₁).

2. Выполним все нужные действия над точкой P.

3. Вернёмся к исходной системе координат.

Сдвиг всей картинки на величину –x₁ и –y₁:

сдвиг действия возврат

Есть отдельные сокращённые матрицы для сдвига, масштаба и поворота относительно любой точки. Смысл – сократить количество операций умножения.

Например.

– результат – это матрица размером 3х3.

Результат умножения таких матриц имеет вид:

Пользоваться перемноженными матрицами можно, если используется не очень быстрая ЭВМ. Причём это касается в первую очередь видеосистемы (не успевает выполнить умножение за время регенерации кадров). Во всех остальных случаях пользоваться упрощёнными формулами не имеет смысла.

Очень часто применяется способ упрощения реализации поворота. От кадра к кадру угол меняется не более чем на 1 градус. В этом случае косинус близок к 1, то есть cos  1, при   1:

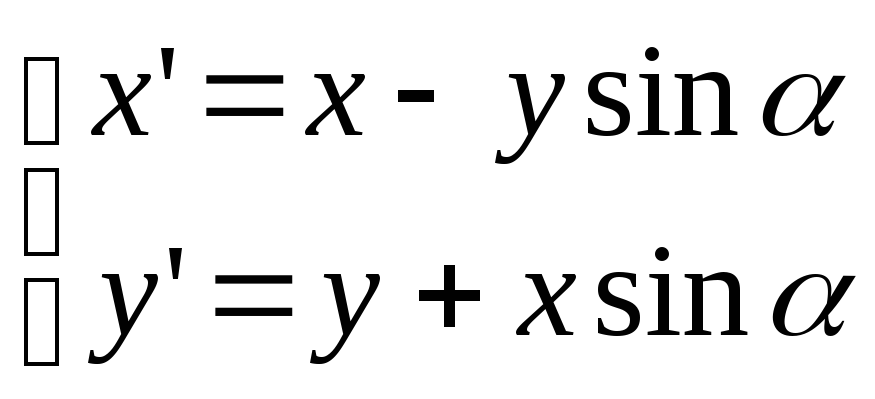
На каждом шаге погрешность очень маленькая, однако если количество оборотов достигнет двух и более, то погрешность может достигнуть веских величин, поэтому пройдя полный круг 360, нужно вернуться к исходному положению точки, то есть погасить погрешность.