Опорную точку переносят в начало координат картинной плоскости. Мировые координаты

правосторонние. Выполняется сдвиг для получения параллельности грани видимого объёма по осям. Нужно выполнить поворот, при котором вектор нормали VNP совпадёт с отрицательной полуосью оси Z.

Поворот такой, чтобы вектор нормали совпал с отрицательной осью Z. Первый поворот до совпадения с полуосью Z. Второй поворот до совпадения с осью Y (положительное направление).

Мировые координаты правосторонние. Их переводят в видовые левосторонние. Выполняется сдвиг для получения параллельности граней осям видовой системы координат видимого объёма. Получение канонического видимого объёма. Преобразования в единичный куб предусматривает сдвиг и масштабирование. Получение видимого объёма.

Воспользуемся формальными записями на каждый шаг.

1. Перенос. Описывается матрицей T.

T(-X_VNP,-Y_VNP,-Z_VNP,1).

2. Поворот до совпадения с осью Z. Нужно выполнить:

поворот вокруг Y: R_y(),

поворот вокруг X: R_x(), то есть R_y()R_x().

3. Поворот вокруг оси Z. R_z()

4. Переход к левосторонней системе координат.

5. Сдвиг по оси Z. В общем случае:

Для ортографических проекций a₁ = b₁ = 0 и это пустая операция. a₁ = b₁ определяются из положения начала координат.

Перед этой операцией видимый объём не является кубом. Нужно пронормировать и сдвинуть.

Штрих потому, что координаты подвергались преобразованиям.

Левый нижний угол будет совпадать с началом видовой плоскости.

– нормирование по всем трём координатам.

Выполнение такой операции и даёт канонический видимый объём – куб. Все эти операции выполняются в заданной последовательности и можно получить общую формулу произвольной проекции.

Чисто формально, выполнив последовательность этих умножений, мы получим произвольную проекцию объекта на плоскость.

Произвольная центральная проекция.

Логическая последовательность действий та же, что и в предыдущем пункте. Разница заключается в другом виде видимого объёма.

Канонический видимый объём задаётся уравнением:

У произвольного видимого исходного объёма пирамида асимметрична. Преобразования состоят из следующих шагов:

1. Перенос центра проекции в начало координат.

2. Поворот до совмещения вектора нормали с отрицательной полуосью z.

3. Поворот относительно оси Z.

4. Переход к левосторонней системе координат.

5. Сдвиг оси видимого объёма до совпадения с осью Z.

6. Получение канонического видимого объёма за счёт сдвига и масштабирования (здесь не куб, а пирамида).

Отличия:

0. Отличие в описании центральной проекции заключается в другом виде первой матрицы сдвига. Координаты центра проекции относительно опорной точки VRP(VRP_x,VRP_y,VRP_z); будут отличаться и будут COP(COP_x, COP_y, COP_z)

Тогда матрица сдвига будет:

T(*)

3. Поворот аналогичен:

вокруг Y

вокруг X

вокруг Z

Переход от правосторонней системы координат к левосторонней – та же матрица.

4. Для центральной проекции:

Ось видимого объёма не совпадает с видовой

осью.

VRP’_z – пересечение с Z.

А – пересечение плоскости YvOZv с осью видимого объёма.

Точка А в видовых координатах имеет координаты:

После преобразования сама точка будет иметь координаты:

Центр симметрии окна будет иметь координаты:

Для симметричности окна надо совместить точку А с точкой С. Тогда VRP’ = (0,0,VRP’_z) будет иметь такие координаты:

Е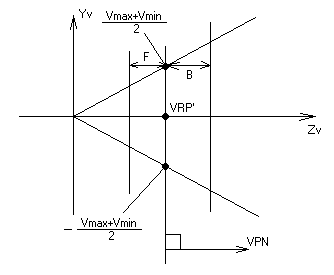сли нарисовать, то мы получим симметричное окно относительно оси OZ.

Эти действия выполняют, чтобы получить симметричность видимого объёма относительно OZ. Только здесь координаты с разницей a₂ и b₂. Симметрию по каждой из проекций:

То есть противоположные грани симметричны, но имеют разный наклон. Необходимо ограничить Zmax единицей. Нормирование по всем трём координатам и будет являться переходом к каноническому видимому объёму (смотри его описание).

Нормирование, выполненное по всем трём координатам с различными коэффициентами:

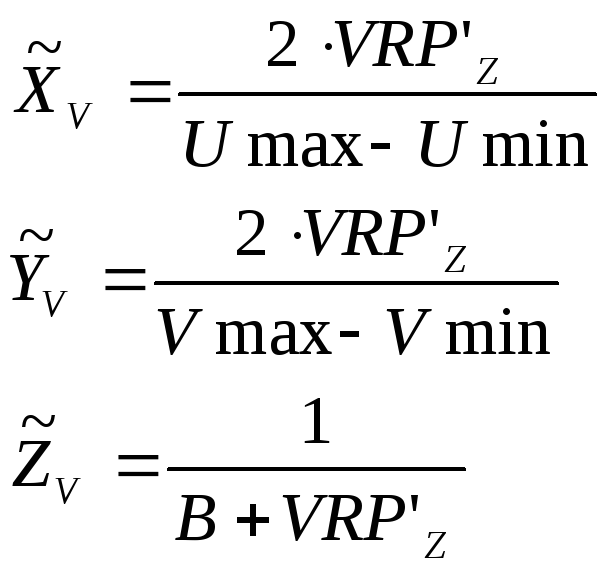
Так как , то точка у канонического объёма проходит через 1.

Матрица перехода к каноническому объёму S:

, где “~” – это не координаты, а коэффициенты.

Тогда полная матрица получения произвольной центральной проекции будет иметь вид: