
- •Сборник
- •Владикавказ
- •Содержание
- •Лабораторная работа № 1 Освоение интерфейса пакета Mathcad
- •II. Цель работы.
- •III. Порядок выполнения работы
- •II. Алгоритм решения системы уравнений с помощью встроенной функции Given…Find приведено на Рис. 1.6.
- •IV. Выполнение работы.
- •VI. Контрольные вопросы.
- •Назад лабораторная работа № 2 «Вычисления в пакете Mathcad. Матрицы»
- •I. Цель работы:
- •II. Теоретическая часть.
- •1. Создание матриц.
- •3. Решение матричных уравнений.
- •4. Оператор векторизации
- •5. Решение дифференциальных уравнений.
- •III. Порядок выполнения работы
- •IV. Выполнение работы.
- •V. Содержание отчета
- •VI. Контрольные вопросы.
- •VIII. Варианты заданий.
- •Назад лабораторная работа № 3 «Вычисления в пакете Mathcad.Интерполяция и Регрессия»
- •I. Цель работы:
- •II. Теоретическая часть.
- •1. Интерполяция.
- •2. Регрессия.
- •4. Элементы математической статистики.
- •III. Порядок выполнения работы
- •IV. Выполнение работы.
- •V. Ход работы.
- •VI. Содержание отчета
- •VII. Контрольные вопросы.
- •IX. Варианты заданий.
- •Назад лабораторная работа № 4 «Вычисления в пакете Mathcad»
- •I. Цель работы:
- •II. Теоретическая часть.
- •1. Решение систем уравнений.
- •2. Приближенное решение уравнений и систем уравнений.
- •3. Исследование функции на экстремум.
- •4. Рекурсивные вычисления.
- •III. Порядок выполнения работы.
- •IV. Выполнение работы.
- •V. Ход работы.
- •VI. Содержание отчета
- •VII. Контрольные вопросы.
- •IX. Варианты заданий.
- •Назад лабораторная работа № 5 Символьные вычисления в Mathcad
- •I. Цель работы.
- •II. Теоретическая часть.
- •III. Порядок выполнения работы
- •IV. Выполнение работы.
- •V. Ход работы.
- •VI. Содержание отчета
- •VII. Контрольные вопросы.
- •IX. Варианты заданий.
- •Назад лабораторная работа № 6
- •Назад лаборат0рная работа № 7 Решение дифференциальных уравнений в функции одной переменной на заданном отрезке методом Рунге-Кута в среде mathcad
- •Назад лаборат0рная работа № 8 Создание анимации в среде mathcad
- •Назад список литературы.
3. Решение матричных уравнений.
Матричные уравнения представляют собой, как правило, систему линейных алгебраических уравнений вида А*Х=В и решаются путем обращения матрицы коэффициентов Х=А-1*В (см. Рис. 2.5.).
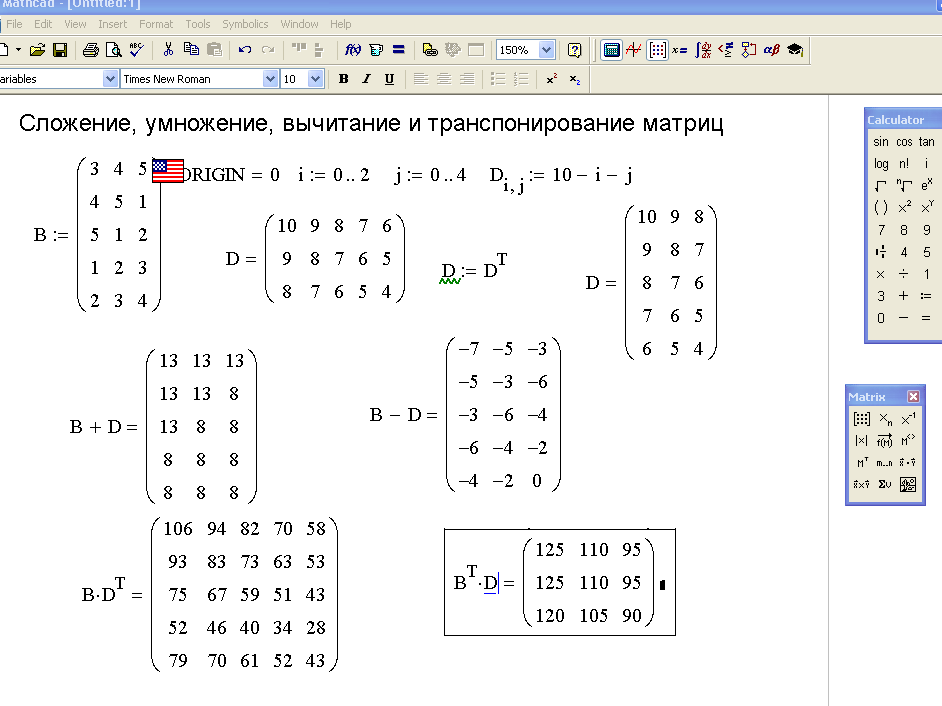
Рис. 2.2. Умножение, сложение, вычитание и транспонирование матриц.
Символьные операции с матрицами можно производить с помощью команд меню Symbolics (Символьные вычисления) и вводом символьного знака равенства (→). В примерах на рис. 2.6. используется только символьный знак равенства.
Р ис.
2.3. Произведение векторов.
ис.
2.3. Произведение векторов.
При выполнении символьных операций с матрицами необходимо помнить, что если какому-либо символу ранее присвоено численное значение, то при наличии символьного знака равенства этот символ участвует в символьных расчетах как число. Если символу ранее присвоено значение вектора или матрицы, то символьные вычисления с его участием становятся невозможными. В этих случаях для символьных вычислений надо использовать команды меню Symbolics (см. Рис.2.6.).
Р ис.
2.4.
Операции
с
матрицами
в
Mathcad.
ис.
2.4.
Операции
с
матрицами
в
Mathcad.
4. Оператор векторизации
Mathcad допускает указывать в качестве аргумента функции не только числа но и вектора. При этом вычисляется значение функции для всех элементов вектора.

Рис. 2.5. Решение системы алгебраических линейных уравнений путем обращения матрицы коэффициентов.
Если аргумент функции — матрица, то, чтобы вычислить значения функции, всех элементов матрицы, надо использовать оператор векторизации.
1. Введите выражение или функцию. 2. Выделите курсором в виде синего уголка необходимую часть выражения (чаще всего выражение целиком).
3 .
На
математической
панели
щелкните
на
кнопке
Vector
and
Matrix
.
На
математической
панели
щелкните
на
кнопке
Vector
and
Matrix
Рис. 2.6. Символьные операции с матрицами
Toolbar (Панель векторов и матриц), а в открывшейся панели — на
кнопке Vectorize (Векторизация). Над выделенной частью выражения появится стрелка — символ операции векторизации.
4. Нажмите клавишу =(равно).
Оператор
векторизации
изменяет
смысл
векторной
или
матричной
операции.
В екторизация
означает
выполнение
однотипной
операции,
екторизация
означает
выполнение
однотипной
операции,
Рис. 2.7. Операции векторизации предписанной выражением, со всеми элементами массива.
Например,
![]() —
операция
невозможная,
если
А
—
вектор
или
матрица,
но,
если,
А аргу-
мент
функции
он
может
быть
вектором,
и
функция,
как
и
в случае
дискретной
пере-
менной,
вычисляется
для
всех
элементов
вектора. Если
аргумент
функции
—
мат-
рица,
необходимо
применение
оператора векторизации,
чтобы
выполнить
то
же
самое,
то
есть
вычислить функцию
для
всех
элементов
матрицы
(в
нашем
случае-
это
корень квадратный
из
каждого
элемента
матрицы
А).
В
случае
перемножения
матриц
А*В
—
это
матричное
произведение,
а
—
операция
невозможная,
если
А
—
вектор
или
матрица,
но,
если,
А аргу-
мент
функции
он
может
быть
вектором,
и
функция,
как
и
в случае
дискретной
пере-
менной,
вычисляется
для
всех
элементов
вектора. Если
аргумент
функции
—
мат-
рица,
необходимо
применение
оператора векторизации,
чтобы
выполнить
то
же
самое,
то
есть
вычислить функцию
для
всех
элементов
матрицы
(в
нашем
случае-
это
корень квадратный
из
каждого
элемента
матрицы
А).
В
случае
перемножения
матриц
А*В
—
это
матричное
произведение,
а
![]() —
это попарное
произведение
элементов
матриц
А
и
В
с
одинаковыми
индексами. Все
массивы
под
знаком
векторизации
должны
быть
одного
размера, так
как
операция
над
всеми
массивами
производится
поэлементно.
Примеры
использования
векторов
или
матриц
в
качестве
аргументов
функций
приведены
на
рис.
2.7.
—
это попарное
произведение
элементов
матриц
А
и
В
с
одинаковыми
индексами. Все
массивы
под
знаком
векторизации
должны
быть
одного
размера, так
как
операция
над
всеми
массивами
производится
поэлементно.
Примеры
использования
векторов
или
матриц
в
качестве
аргументов
функций
приведены
на
рис.
2.7.
Внимание: Если аргумент — вектор, векторизация не нужна. Если аргумент — матрица, векторизация нужна.
