
- •1. Первообразная. Неопределённый интеграл. Таблица неопределённых вариантов.
- •2. Замена переменной в неопределенном интеграле.
- •1) Внесение под знак диф-ла:
- •2) Вынесение из-под знака диф-ла:
- •3.Интегрирование по частям.
- •4. Разложение прав. Рац. Дроби в сумму простейших. Интегрирование рац. Дробей.
- •7777. Интегрирование тригонометрических функций.
- •7. Интегрирование иррац-тей.
- •8. Задачи, приводящие к понятию определения ои
- •9. Определение ои как предела инт суммы. Св ои.
- •11. Инт с перем верхним пределом Формула н-л.
- •11. Замена переменных и интег-ние по частям.
- •11. Геометрические и физические приложения о и
- •13. Нес инт с бескон пред инт-я. Н и от ннеогран ф-й
- •16. Функции нескольких переменных. Предел фмп. . Частные производные
- •20 Частные производные высших порядков.
- •21. Дифференцируемость фмп. Полный дифференциал. Уравнения Касательной и нормали
- •15. Дифференцируемость фмп. Полный дифференциал. Уравнения Касательной и нормали
- •25. Условный экстремум фнп
- •26. Основные понятия теории дифферинциальных уравнений.
- •30. Уравнения в полных дифференциалах
- •31. Линейные ду 1 порядка: однор и неоднор, метод Бернули
- •Подставляем полученное соотношение в исходное уравнение
- •33.Уравнение Бернулли.
- •35. Линейные однородные дифференциальные уравнения с произвольными коэффициентами.
- •36Лду-n: однор и неоднор Линейный диф опер-р его св-ва, св-св реш лду.
- •36 Лоду с постоянными коэффициентами: случай различных действительных корней хар-го Ур-я.
- •При этом многочлен называется характеристическим многочленом дифференциального уравнения.
- •37. Линейные однородные дифференциальные уравнения с постоянными коэффициентами: все корни хар-го Ур-я различны, но есть комплексные
- •При этом многочлен называется характеристическим многочленом дифференциального уравнения.
- •38. Структура общего решения лнду-n. Принцип суперпозиции
- •38. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
- •39. Метод вариации произвольных постоянных.
- •42. Двойные интегралы. Св-ва.
- •43. Тройной интеграл: определение, свойства.
- •45. Вычисление тройных интегралов
- •44 Замена переменной в двойном интеграле.Полярная система координат площ плоской фигуры
- •45. Ти в цилинд. И координатах. Переход в тройном интеграле от декартовой к цилиндрической си-ме коорд
- •45. Ти в сферич. Координатах. Переход в тройном интеграле от декартовой к сферической си-ме коорд.
11. Геометрические и физические приложения о и
y
y = f(x)
xi
a b x
Определение: Длиной дуги называется предел периметра вписанной в нее ломанной, если длина максимал. ломаной стремится к 0. Если предел конечен, то дуга – спрямляемая.
Длина ломаной линии,
которая соответствует дуге, может быть
найдена как
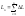 .
.
Тогда длина дуги равна
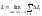 .
.
Из геометрических
соображений:
![]()
В то же время
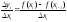
Тогда можно показать,
что
![]() Т.е.
Т.е.
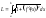
Если уравнение кривой
задано параметрически, то с учетом
правил вычисления производной
параметрически заданной функции,
получаем
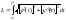 ,
где х = (t)
и у = (t).
,
где х = (t)
и у = (t).
Если задана пространственная кривая, и х = (t), у = (t) и z = Z(t), то
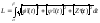
если кривая задана в
полярных координатах, то
![]() ,
= f().
,
= f().
Диф-л дуги: L’(x) = dL/dx = a/√1+f ’2(x)
рис. dL = (a/√(1+f ’2(x)))*dx = √dx2+dy
dL2 = dx2+dy2
13. Нес инт с бескон пред инт-я. Н и от ннеогран ф-й
Пусть функция f(x) определена и непрерывна на интервале [a, ). Тогда она непрерывна на любом отрезке [a, b].
Определение:
Если существует конечный предел
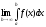 ,
то этот предел называется несобственным
интегралом от функции f(x)
на интервале [a, ).
,
то этот предел называется несобственным
интегралом от функции f(x)
на интервале [a, ).
Обозначение:
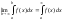
Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
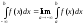
![]()
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
Пример.
![]() -
не существует.
-
не существует.
Несобственный интеграл расходится.
Теорема: Если
для всех х (x
a) выполняется условие
![]() и интеграл
и интеграл
![]() сходится, то
сходится, то
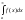 тоже сходится и
тоже сходится и
![]()
![]() .
.
Теорема: Если
для всех х (x
a) выполняется условие
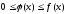 и интеграл
и интеграл
![]() расходится, то
расходится, то
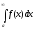 тоже расходится.
тоже расходится.
Теорема: Если
![]() сходится, то сходится и интеграл
сходится, то сходится и интеграл
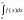 .
.
В этом случае интеграл
![]() называется абсолютно сходящимся.
называется абсолютно сходящимся.
13-14. Нес инт с бескон пред инт-я. Н и от ннеогран ф-й
Пусть
ф-ия f(x)
определена на [a;b)
интегрируема на любом промежутке [a;b- ] и кроме того
] и кроме того
![]() .
Рассмотрим
.
Рассмотрим
![]() Если указанный предел сущ то говорят
что этот предел наз несобственным
Интеграл от ф-ии f(x)
(несобственным интегралом второго рода)
И обознач
Если указанный предел сущ то говорят
что этот предел наз несобственным
Интеграл от ф-ии f(x)
(несобственным интегралом второго рода)
И обознач
![]() анологично если т. a
особенная и
анологично если т. a
особенная и
![]() На промежутке
На промежутке
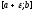 ф-ия интегрируема, то несобственный
интеграл вводится так
ф-ия интегрируема, то несобственный
интеграл вводится так
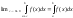 .
Если особой точкой является внутренняя
точка отрезка [a;b)
то под несобственным интегралом
понимается
.
Если особой точкой является внутренняя
точка отрезка [a;b)
то под несобственным интегралом
понимается
![]() .
Подчеркнем что в 3-ем случае
.
Подчеркнем что в 3-ем случае
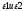 стремятся к нулю независимо друг от
друга. Если указанные пределы сущ то
несобственные интегралы наз сходящимися
а если равны бесконечности или не сущ
то эти интегралы наз росходящимися в
случае если f(x)
неограниченная ф-ия то можно дать
геометрическую интерпритацию несобсятвеных
интегралов второго рода.
стремятся к нулю независимо друг от
друга. Если указанные пределы сущ то
несобственные интегралы наз сходящимися
а если равны бесконечности или не сущ
то эти интегралы наз росходящимися в
случае если f(x)
неограниченная ф-ия то можно дать
геометрическую интерпритацию несобсятвеных
интегралов второго рода.
критерии
Коши и признаки сравнения. Пусть С-
внутренняя точка (особоя) для того чтобы
несобственный
![]() был сходящимся необходимо и достаточно
чтобы для любого
был сходящимся необходимо и достаточно
чтобы для любого
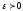 существовала такая
существовала такая
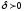 чтобы для любых четырех отрицательных
чисел
чтобы для любых четырех отрицательных
чисел
![]() выполнялось
выполнялось
![]() .
Признак сравнения:
.
Признак сравнения:
Пусть
для всех X из облости
существования выполняется условие
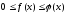 тогда и сходимости несобственного
интеграла
тогда и сходимости несобственного
интеграла
![]() вытекает сходимость несобственного
интеграла
вытекает сходимость несобственного
интеграла
![]() .
И наоборот из расходимости несобственного
интеграла
.
И наоборот из расходимости несобственного
интеграла
![]() следует расходимость несобственнго
интеграла
следует расходимость несобственнго
интеграла
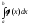 .
.
Теорема:
(предельный признак сходимости): Пусть
на отрезке [a;b)
f(x) и
 (x)
знакоположительные ф-ии
(x)
знакоположительные ф-ии
![]() .
И сущ
.
И сущ
![]() тогда в смысле сходимости оба интеграла
тогда в смысле сходимости оба интеграла
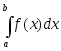 и
и
![]() ведут себя одинаково т.е. одновременно
сходятся и расходятся.
ведут себя одинаково т.е. одновременно
сходятся и расходятся.
