
- •1. Первообразная. Неопределённый интеграл. Таблица неопределённых вариантов.
- •2. Замена переменной в неопределенном интеграле.
- •1) Внесение под знак диф-ла:
- •2) Вынесение из-под знака диф-ла:
- •3.Интегрирование по частям.
- •4. Разложение прав. Рац. Дроби в сумму простейших. Интегрирование рац. Дробей.
- •7777. Интегрирование тригонометрических функций.
- •7. Интегрирование иррац-тей.
- •8. Задачи, приводящие к понятию определения ои
- •9. Определение ои как предела инт суммы. Св ои.
- •11. Инт с перем верхним пределом Формула н-л.
- •11. Замена переменных и интег-ние по частям.
- •11. Геометрические и физические приложения о и
- •13. Нес инт с бескон пред инт-я. Н и от ннеогран ф-й
- •16. Функции нескольких переменных. Предел фмп. . Частные производные
- •20 Частные производные высших порядков.
- •21. Дифференцируемость фмп. Полный дифференциал. Уравнения Касательной и нормали
- •15. Дифференцируемость фмп. Полный дифференциал. Уравнения Касательной и нормали
- •25. Условный экстремум фнп
- •26. Основные понятия теории дифферинциальных уравнений.
- •30. Уравнения в полных дифференциалах
- •31. Линейные ду 1 порядка: однор и неоднор, метод Бернули
- •Подставляем полученное соотношение в исходное уравнение
- •33.Уравнение Бернулли.
- •35. Линейные однородные дифференциальные уравнения с произвольными коэффициентами.
- •36Лду-n: однор и неоднор Линейный диф опер-р его св-ва, св-св реш лду.
- •36 Лоду с постоянными коэффициентами: случай различных действительных корней хар-го Ур-я.
- •При этом многочлен называется характеристическим многочленом дифференциального уравнения.
- •37. Линейные однородные дифференциальные уравнения с постоянными коэффициентами: все корни хар-го Ур-я различны, но есть комплексные
- •При этом многочлен называется характеристическим многочленом дифференциального уравнения.
- •38. Структура общего решения лнду-n. Принцип суперпозиции
- •38. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
- •39. Метод вариации произвольных постоянных.
- •42. Двойные интегралы. Св-ва.
- •43. Тройной интеграл: определение, свойства.
- •45. Вычисление тройных интегралов
- •44 Замена переменной в двойном интеграле.Полярная система координат площ плоской фигуры
- •45. Ти в цилинд. И координатах. Переход в тройном интеграле от декартовой к цилиндрической си-ме коорд
- •45. Ти в сферич. Координатах. Переход в тройном интеграле от декартовой к сферической си-ме коорд.
7777. Интегрирование тригонометрических функций.
1) Интеграл вида
 .
.
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы этого вида
вычисляются с помощью подстановки
 .
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
.
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
 ,
,

Тогда

Таким образом:

Описанное выше преобразование называется универсальной тригонометрической подстановкой.
2) ∫ соsmx*sinnxdx, где m,n – нат. числа
а) пусть m = 2p+1
∫соs2p+1x*sinnxdx = ∫ (1-cos2x)p*sinnxdx*d(sinx) = ∫ (1-U2)p*UndU, если n=2p+1, то синус выносится под знак диф-ла
sin dx = -d(cosx)
б) m = 2p, n=2q
∫соs2px*sin2qdx = ∫((1+cos2x)/2)p*((1-cos2x)/2)q*d(sinx)
3) Интеграл произведения синусов и косинусов различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
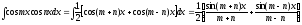


7. Интегрирование иррац-тей.
1. ∫R(x, n√x)dx, R – рац. выражение – над х и n√x проведено конечное число арифмет. операций.
= |x=tk, dx=ktk-∙1dt, k – НОК| = ∫R(tk, t)ktk-1dt
2.
Интеграл вида
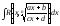 где n- натуральное
число.
где n- натуральное
число.
С помощью подстановки
 функция рационализируется.
функция рационализируется.

Тогда

8. Задачи, приводящие к понятию определения ои
Определение Ньютона: Пусть ф-ция f(x) имеет смысл на [а, b] первообразную F(x), тогда определенным інтегралом ф-ции f(x) на [а, b] называется число F(b) - F(а)
а∫bf(x)dx = F(b) - F(а) = F(x)|ab
Задачи: (для Римана)
-
площадь криволинейной трапеции
-
масса отрезка с переменной плотностью
Определение:
Если при любых разбиениях отрезка [a,
b] таких, что maxxi
0 и произвольном выборе точек i
интегральная сумма
 стремится к пределу S,
который называется определенным
интегралом от f(x)
на отрезке [a, b].
стремится к пределу S,
который называется определенным
интегралом от f(x)
на отрезке [a, b].
Обозначение :

а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.
Определение: Если для функции
f(x) существует
предел

 то функция называется интегрируемой
на отрезке [a, b].
то функция называется интегрируемой
на отрезке [a, b].
Также верны утверждения:

![]()
9. Определение ои как предела инт суммы. Св ои.
-

-
∫abkdx = k(b-a)- вытекает из определения, т.к. ∑k=0n-1f(сиj)дельтахj =
∑k=0n-1 kдельтахj =k ∑k=0n-1 дельтахj = k(b-a)
-
 -
св-во линейности
-
св-во линейности -
Пусть ф-ция f(x) кусочно-постоянная на отрезке [a,b], т.е. сущ. разбиение отрезка [a,b] на (xk, xk+1) ф-ция f(x) принимает постоян зн-ние lk:
∫abf(x)dx = ∑ab lk дельта xk
-

-
 - свойство аддитивности
- свойство аддитивности -
Если f(x) (x) на отрезке [a, b] a < b, то

-
Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

Определение:
Если при любых разбиениях отрезка [a,
b] таких, что maxxi
0 и произвольном выборе точек i
интегральная сумма
 стремится к пределу S,
который называется определенным
интегралом от f(x)
на отрезке [a, b].
стремится к пределу S,
который называется определенным
интегралом от f(x)
на отрезке [a, b].
О. Если для функции
f(x) существует
предел

 то функция называется интегрируемой
на отрезке [a, b].
то функция называется интегрируемой
на отрезке [a, b].
Также верны утверждения:

![]()
