38. Структура общего решения лнду-n. Принцип суперпозиции

Постановка задачи. Найти общее решение линейного дифференциального уравнения -го порядка с постоянными коэффициентами, (1)

где .

Принцип суперпозиции. Если правая часть уравнения (1) есть сумма нескольких функций

и  – какое-нибудь частное решение каждого из уравнений, (2)

то в силу линейности уравнения (1) его общее решение имеет вид,где  – общее решение однородного уравнения.

1. Находим фундаментальную систему решений и общее решение  однородного уравнения.

2. Для каждого неоднородного уравнения (2) находим частное решение .

Записываем ответ.

38. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.

Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения.

Различают следующие случаи:

I. Правая часть линейного неоднородного дифференциального уравнения имеет вид: где 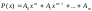- многочлен степени m. Тогда частное решение ищется в виде:

Здесь Q(x)- многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число  является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.

II. Правая часть линейного неоднородного дифференциального уравнения имеет вид:

Здесь Р₁(х) и Р₂(х) – многочлены степени m₁ и m₂ соответственно.

Тогда частное решение неоднородного уравнения будет иметь вид:

где число r показывает сколько раз число является корнем характеристического уравнения для соответствующего однородного уравнения, а Q₁(x) и Q₂(x) – многочлены степени не выше m, где m- большая из степеней m₁ и m₂.

Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию.

Т.е. если уравнение имеет вид: , то частное решение этого уравнения будет 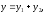где у₁ и у₂ – частные решения вспомогательных уравнений

и

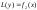
39. Метод вариации произвольных постоянных.

Для этого сначала находят общее решение соответствующего однородного уравнения в виде:

Затем, полагая коэффициенты C_i функциями от х, ищется решение неоднородного уравнения:

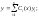
Можно доказать, что для нахождения функций C_i(x) надо решить систему уравнений:

42. Двойные интегралы. Св-ва.

Задачи:

1)V цилиндроида

2) Масса пластинки с поверхностной плотностью ρ(х,у). толщиной принебрегаем.

Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой

f(x, y) = 0.

y

0 x

Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью . Если выбрать точки области без учета точек, лежащих на кривой, область будет называется незамкнутой область .

С геометрической точки зрения  - площадь фигуры, ограниченной контуром.

Разобьем область  на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние х_i, а по оси у – на у_i. Вообще говоря, такой порядок разбиения наобязателен, возможно разбиение области на частичные участки произвольной формы и размера.

Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны S_i = x_i  y_i .

В каждой частичной области возьмем произвольную точку Р(х_i, y_i) и составим интегральную сумму

где f – функция непрерывная и однозначная для всех точек области .

Если бесконечно увеличивать количество частичных областей _i, тогда, очевидно, площадь каждого частичного участка S_i стремится к нулю.

Определение: Если при стремлении к нулю шага разбиения области  интегральные суммы имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области .

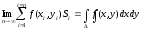
42. Двойные интегралы. Св-ва.С учетом того, что S_i = x_i  y_i получаем:

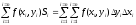
В приведенной выше записи имеются два знака , т.к. суммирование производится по двум переменным х и у.

Т.к. деление области интегрирования произвольно, также произволен и выбор точек Р_i, то, считая все площади S_i одинаковыми, получаем формулу:

Свойства двойного интеграла.

1)

2)

3) Если  = ₁ + ₂, то

4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования.

5) Если f(x, y)  0 в области , то .

6) Если f₁(x, y)  f₂(x, y), то .

7) .

41-42. вычисление двойных интегралов: а прямоуг б) крив область

41) Теорема: Пусть z = f(x,y) – ограниченная функция, заданная на прямоугольнике R = [a,b;c,d], и существует двойной интеграл по этому прямоугольнику Если для  X [a,b] существует одномерный интегралто  повт интеграл Док-во: Разобьем отрезки ab и cd отрезками a=x₀<x₁<…<x_n=b, c=y₀<y₁<…<y_n=d. Рассмотрим теперь частичный прямоугольник R_ik=[x_i,x_i+1;y_i,y_i+1] m_ik=inf f(x,y) M_ik=sup f(x,y) Rik Rik

На промежутке [x_i;x_i+1] возьмём точку . Будем рас- сматривать точки, лежащие на прямой x = .Получаем следующее неравенство m_ik f(;y) M_ik y_k y y_k+1 Проинтегрируем его по отрезку [y_k; y_k+1]

42) Пусть в плоскости XOY задана плоскость Д, ограничен-ная следующими

кривыми: y=₁(x) a  x  a – снизу; y=₂(x) a  x  b – сверху; x = a – слева; x = b – справа; Тогда имеет место следующая теорема. Теорема: Если функция

41-42. вычисление двойных интегралов: а прямоуг б) крив область

f(x;y) задана в области Д такова, что существует двойной интеграл для любого фиксированного x [a ; b] существует одно- мерный интеграл то тогда существует повторный интеграл Доказательство:

Обозначим c=inf ₁(x) a  x  b; d=max ₁(x) a  x  b и рассмотрим прямоугольник R=[a,b;c,d]Д. P=R\Д (раз- ность множеств). Построим вспомогательную функциюРассмотримПолучаем равенство: