6.2. Численные методы

Задачи для нелинейных уравнений или даже линейные задачи, но в областях сложной формы редко удается решить классическими методами. Основным способом решения таких задач являются численные методы. Среди них чаще всего применяют разностные методы благодаря их универсальности и наличию хорошо разработанной теории.

Для применения разностного метода в области изменения переменных G (r, t) вводят некоторую сетку. Все производные, входящие в уравнение, и краевые условия заменяют разностями (или другими алгебраическими комбинациями) значений функции u(r, t) в узлах сетки. Получающиеся при этом алгебраические уравнения называют разностной схемой. Решая полученную алгебраическую систему, найдем приближенное (разностное) решение в узлах сетки.

Пример. Составим простейшие разностные схемы для одномерной задачи линейной теплопроводности на ограниченном отрезке:

, 0  x  a, 0  t  T, (6.6)

u(x, 0)=(x) – начальное условие, (6.6,а)

u(0, t)= – краевое условие,

u(a, t)= – внутренние источники тепла.

Решение ищется в области .

Введем в G прямоугольную сетку (для простоты равномерную), образованную пересечением линий x_п = nh, 0 п N, и t_m = m, 0 m M; величины h,  являются шагами сетки по переменным x, t. Значения функции в узлах сетки будем обозначать .

Заменим в уравнении (6.6) производную u_t разностным отношением . Производную также можно заменить разностным отношением. Но здесь возможны разные варианты, которые приводят к явной и неявной схемам решения задачи. К явной схеме решения задачи приводит аппроксимация производной уравнением вида 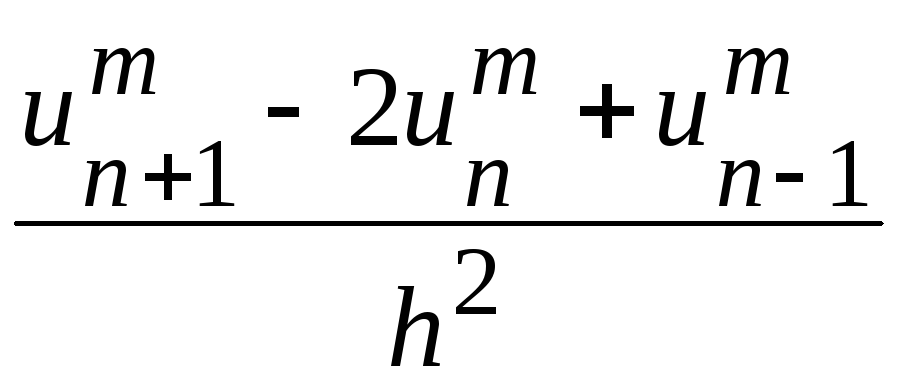,а к неявной  уравнением 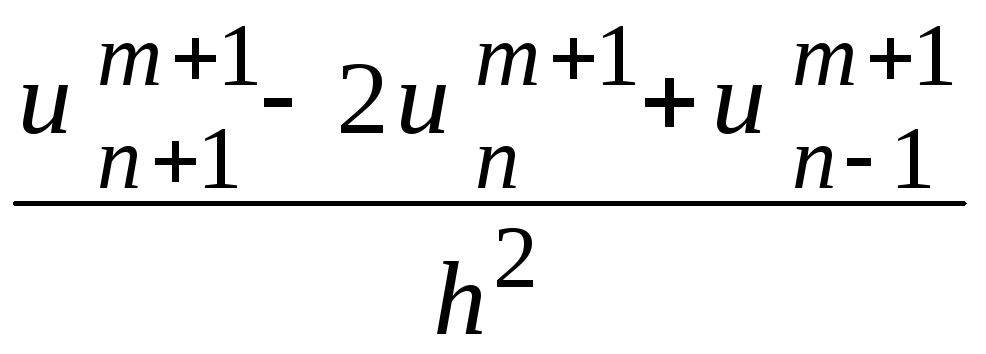. При явной схеме уравнение (6.6) принимает вид

. (6.7)

Это послойный алгоритм вычислений. В этой схеме на исходном m = 0 слое решение известно в силу начального условия (6.6, а). Каждое последующее значение на m+1 слое определится из уравнения (6.7) по известным значениям переменной на предыдущем слое.

. (6.8)

При неявной схеме уравнение (6.6) принимает вид

, 1 n N-1. (6.9)

Число уравнений (6.9) меньше числа неизвестных , 0  n N; недостающие уравнения выводятся из начальных и граничных условий (6.6, а):

, 0  n  N, , .

Уравнение (6.9) неявной схемы содержит в каждом уравнении несколько неизвестных значений функции на новом слое; подобные схемы называются неявными. Для вычисления переменных перепишем систему (6.9) с учетом краевых условий по следующей форме:

, 1  n  N-1, (6.10)

, .

На каждом слое система (6.10) представляет собой систему линейных уравнений для определения величин , правые части этих уравнений известны, поскольку содержат значения решения с пре­дыдущего слоя. Матрица линейной системы трехдиагональна, и решение можно вычислить алгебраической прогонкой.