
- •5.1. Классический способ определения величины парового потока
- •5.2. Наглядно-смысловой способ определения величины парового потока
- •5.3. Составление блок-схемы модели самовара
- •6. Моделирование процессов, описываемых в частных производных
- •6.1 Физический смысл уравнения теплопроводности
- •6.2. Численные методы
- •6.3. Метод прогонки
- •6.4. Комбинированный метод решения смешанной краевой задачи
- •7. Моделирование случайных воздействий
- •7.1. Моделирование дискретных случайных величин
V2
Рвн
V1






 Pa
Pa
![]()

1
0,2


20 100 Т С
Рис 5.1. Физическая модель
самовара
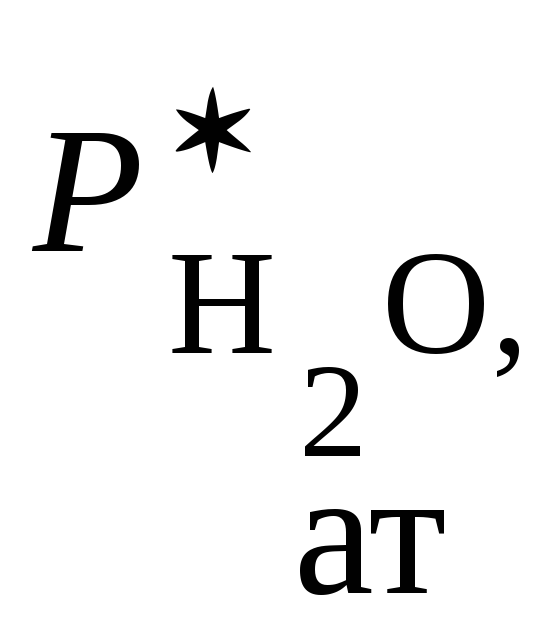
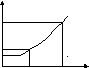
Рис.5.2 График зависимости парциального давления насыщенного водяного пара от температуры
Составим уравнение теплового баланса:
![]() ,
(5.1)
,
(5.1)
где qвх – мощность нагревателя.
Количество тепла, необходимое для нагрева воды массой Мв с удельной теплоемкостью Cв на T - T0 С,
![]() ,
(5.2)
,
(5.2)
где qвых – тепловой поток, затраченный на испарение воды;
qвых = rgп,
где r = 550 ккал/кг - удельная теплота парообразования.
gп – весовой расход паров воды.
Рассмотрим два подхода классический и наглядно-смысловой к определению gп.
5.1. Классический способ определения величины парового потока
Весовой расход паро-воздушной смеси, выводимой из самовара через сужающее устройство (дырочку в крышке) найдем по формуле [4]:
![]() ,
(5.3)
,
(5.3)
где Pвн – давление в аппарате;
Ра – атмосферное давление;
kv – коэффициент, определяемый видом сужающего устройства (считается известным).
Расход
пара, выводимого из аппарата, прямо
пропорционален концентрации пара в
смеси, а следовательно, отношению
парциального давления паров воды
![]() к общему давлению в аппарате
P.
к общему давлению в аппарате
P.
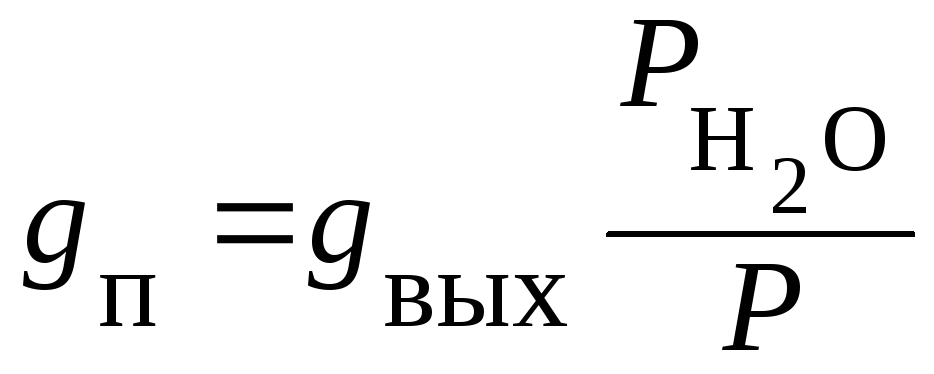 .
(5.4)
.
(5.4)
Таким
образом, для определения
![]() нам необходимо знать общее давление в
аппарате и парциальное давление паров
воды, которые нам не известны. Значения
этих параметров можно найти из условия
материального баланса:
нам необходимо знать общее давление в
аппарате и парциальное давление паров
воды, которые нам не известны. Значения
этих параметров можно найти из условия
материального баланса:
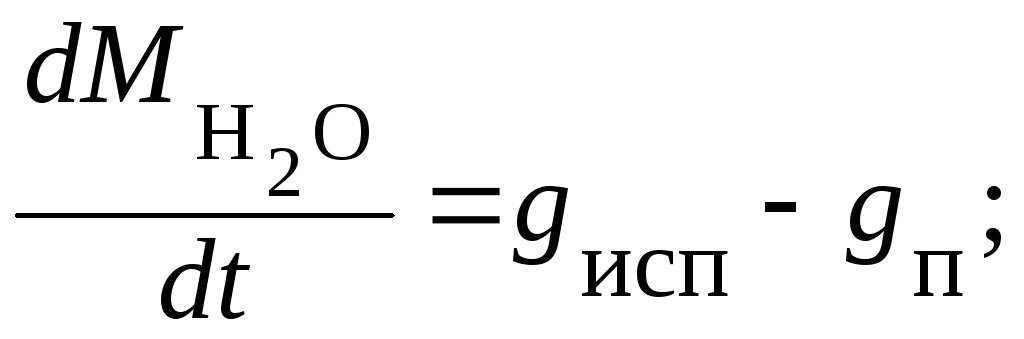 (5.5)
(5.5)
![]() (5.6)
(5.6)
где
![]() ,
,
![]() – масса паров воды и воздуха в аппарате,
соответственно,
– масса паров воды и воздуха в аппарате,
соответственно,
![]()
![]() –
весовой
расход воды из аппарата.
–
весовой
расход воды из аппарата.
![]() (5.7)
(5.7)
![]() – паровой поток
с поверхности воды.
– паровой поток
с поверхности воды.
ky – коэффициент массопередачи; [8];
S – площадь поверхности воды;
![]() –
парциальное
давление насыщенного пара.
–
парциальное
давление насыщенного пара.
Проинтегрировать (численно) уравнение (4.6) не представляет проблем, а об интегрировании уравнения (4.5) следует поговорить особо.
Если
в уравнение (4.5) подставить
![]() из (4.7), а массу
из (4.7), а массу
![]() выразить
из
уравнения состояния газа
выразить
из
уравнения состояния газа
![]() ,
где
,
где
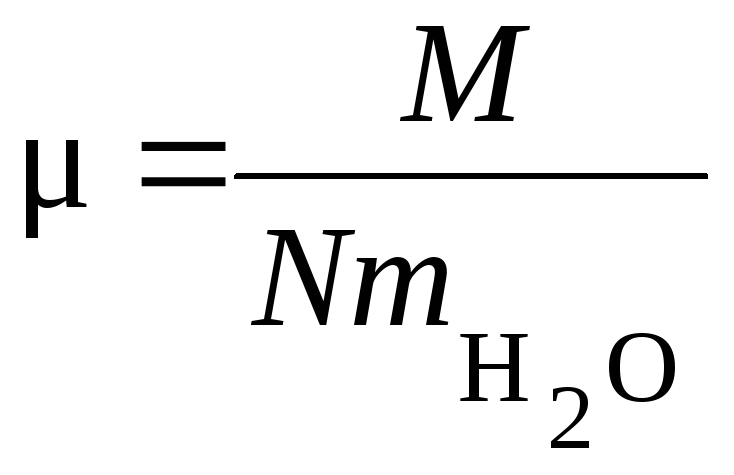 –
число молей в аппарате, N
– число
Авогадро, то получим дифференциальное
уравнение для расчёта
–
число молей в аппарате, N
– число
Авогадро, то получим дифференциальное
уравнение для расчёта
![]() которое, в принципе, нетрудно
проинтегрировать.
которое, в принципе, нетрудно
проинтегрировать.
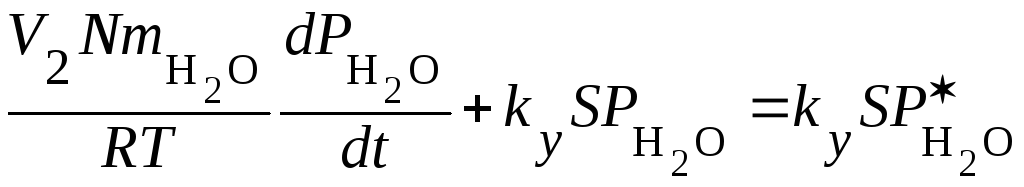 .
(5.8)
.
(5.8)
Но
следует принять во внимание, что ky
настолько
велико, что постоянная времени данного
уравнения на два порядка меньше
постоянной времени в дифференциальном
уравнении теплового баланса. Действительно,
известно, что влажность воздуха в
чайнике близка к насыщению. Поэтому,
если численно интегрировать уравнение
(4.5), то шаг интегрирования придется
взять
![]() от постоянной времени уравнения (4.5),
а это означает, что время счета модели
возрастет более чем на два порядка по
сравнению с вариантом, при котором
от постоянной времени уравнения (4.5),
а это означает, что время счета модели
возрастет более чем на два порядка по
сравнению с вариантом, при котором
![]() находится, как решение уравнения для
установившегося режима при заданной
скорости изменения
находится, как решение уравнения для
установившегося режима при заданной
скорости изменения
![]() .
То есть на каждом шаге интегрирования
считается
.
То есть на каждом шаге интегрирования
считается
![]() .
Рассмотренный подход к решению уравнения
вполне корректен, хотя трудоёмкость
его достаточно велика, а точность во
многом зависит от точности коэффициента
.
Рассмотренный подход к решению уравнения
вполне корректен, хотя трудоёмкость
его достаточно велика, а точность во
многом зависит от точности коэффициента
![]() ,
значение которого точно определить
трудно, так как массопередача зависит
не только от свойств продуктов, но и от
аппаратурного оформления. Поэтому ниже
прилагается способ, основанный на
понимании сущности процесса, а не на
формальном его описании.
,
значение которого точно определить
трудно, так как массопередача зависит
не только от свойств продуктов, но и от
аппаратурного оформления. Поэтому ниже
прилагается способ, основанный на
понимании сущности процесса, а не на
формальном его описании.
5.2. Наглядно-смысловой способ определения величины парового потока
В
разделе 4.1 было показано, что парциальное
давление пара в аппарате примерно равно
давлению насыщенного пара
![]() .
Из уравнения состояния газа
.
Из уравнения состояния газа
![]() видно,
что давление пара прямо пропорционально
количеству молей его в единице объёма,
видно,
что давление пара прямо пропорционально
количеству молей его в единице объёма,
![]() .
(5.9)
.
(5.9)
Так
как общее давление в аппарате определяет
общее количество молей в единице объёма,
то это можно интерпретировать следующим
образом: давление пара определяет долю
объёма, занимаемую в
![]() .
.
Действительно,
чем больше
![]() ,
тем больше молей паров в единице объёма,
а это можно трактовать и так, что больше
доля, занимаемая молекулами пара, в
парогазовой смеси. Из сказанного
следует, что объём, занимаемый парами
воды, прямо пропорционален
,
тем больше молей паров в единице объёма,
а это можно трактовать и так, что больше
доля, занимаемая молекулами пара, в
парогазовой смеси. Из сказанного
следует, что объём, занимаемый парами
воды, прямо пропорционален
![]() .
.
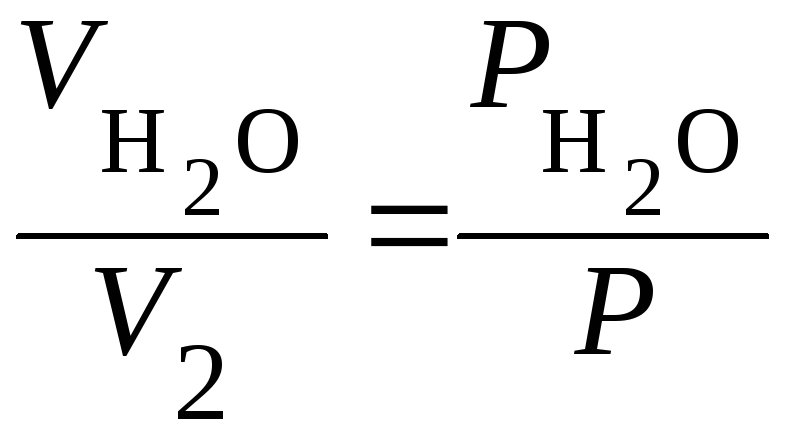 .
(5.10)
.
(5.10)
Так
как
![]() ,
то скорость вытеснения парогазовой
смеси из аппарата пропорциональна
скорости изменения
,
то скорость вытеснения парогазовой
смеси из аппарата пропорциональна
скорости изменения
![]() .
А это легко найти из известной зависимости
давления насыщенного пара от давления
(рис 5.2) и скорости изменения температуры
(5.1, 5.2). Действительно, аппроксимировав
зависимость
.
А это легко найти из известной зависимости
давления насыщенного пара от давления
(рис 5.2) и скорости изменения температуры
(5.1, 5.2). Действительно, аппроксимировав
зависимость
![]() от температуры Т
полиномом, получим дифференцируемую
функцию
от температуры Т
полиномом, получим дифференцируемую
функцию
![]() .
Использовав эту функцию, получим
выражение для объёмного расхода
вытесненного пара:
.
Использовав эту функцию, получим
выражение для объёмного расхода
вытесненного пара:
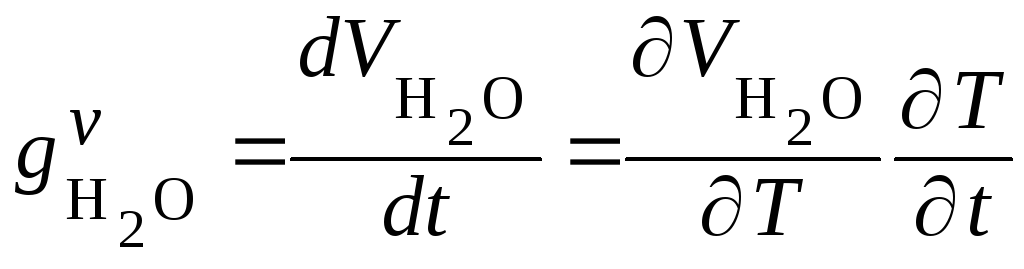 .
(5.11)
.
(5.11)
Используя (5.10), получим
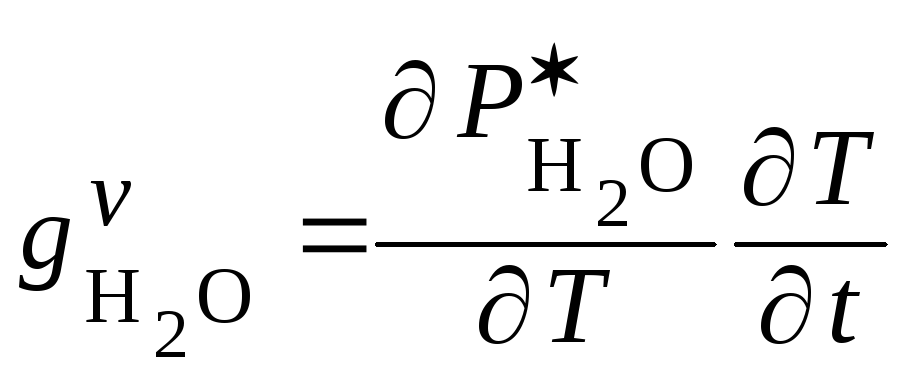 .
(5.12)
.
(5.12)
Так
как объемный расход парогазовой смеси
равен объёмному расходу вытеснившего
его пара
![]() ,
то
,
то
![]() .
.
Зная объёмные расходы пара и воздуха, можно найти весовые расходы каждого из этих компонентов, так как зависимость плотности насыщенного пара от температуры задаётся в справочниках, а плотность воздуха в аппарате можно найти, зная парциальные давления пара и воздуха в аппарате:
![]()
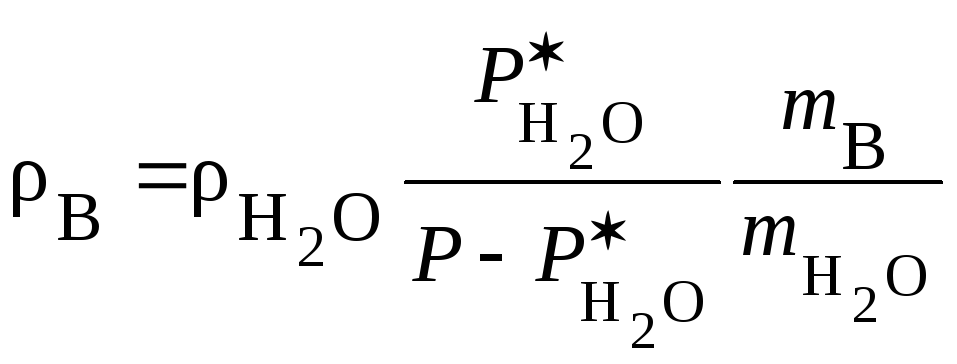 ,
(5.13)
,
(5.13)
где
![]()
мольные массы воздуха и паров воды
соответственно.
мольные массы воздуха и паров воды
соответственно.
Формула
(5.13) получена из уравнений состояния
газа для пара и воздуха, в которых
количество молей выражено через массы
каждого из компонентов
![]() .
.
