
4.3. Метод простых итераций
Есть случаи, когда уравнение (4.1) можно заменить эквивалентным ему уравнением
![]() ,
иначе
,
иначе
![]() (4.2)
(4.2)
где
![]() .
.
Выберем
некоторое нулевое приближение
![]() и вычислим дальнейшие приближения по
формулам
и вычислим дальнейшие приближения по
формулам
![]() ,
n
= 0, 1, 2, … (4.3)
,
n
= 0, 1, 2, … (4.3)
Очевидно,
если
![]() стремится
к некоторому пределу
стремится
к некоторому пределу
![]() ,
то этот предел есть корень исходного
уравнения.
,
то этот предел есть корень исходного
уравнения.
Исследуем
условия сходимости. Если ![]() имеет непрерывную производную, тогда
имеет непрерывную производную, тогда
![]()
![]()
![]()
![]() ,
(4.4)
,
(4.4)
где
точка
лежит между точками
![]() и
и
![]() .
Поэтому, если всюду
.
Поэтому, если всюду
![]()
q
< 1, то
отрезки
q
< 1, то
отрезки
![]() убывают не медленнее, чем члены
геометрической прогрессии со знаменателем
q
< 1,
и последовательность
убывают не медленнее, чем члены
геометрической прогрессии со знаменателем
q
< 1,
и последовательность
![]() сходится
при любом нулевом приближении (рис.
4.3 а,
в).
Если
|(
сходится
при любом нулевом приближении (рис.
4.3 а,
в).
Если
|(![]() )|
>1,
то в силу непрерывности
и в некоторой окрестности корня
выполняется это неравенство; в этом
случае итерации не могут сходиться.
Если |(
)|
>1,
то в силу непрерывности
и в некоторой окрестности корня
выполняется это неравенство; в этом
случае итерации не могут сходиться.
Если |(![]() )|
<
1,
но вдали от корня |
(x)|
>
1,
то итерации сходятся при условии, что
нулевое приближение выбрано достаточно
близко к корню; при произвольном нулевом
приближении сходимости может не быть.
)|
<
1,
но вдали от корня |
(x)|
>
1,
то итерации сходятся при условии, что
нулевое приближение выбрано достаточно
близко к корню; при произвольном нулевом
приближении сходимости может не быть.
Очевидно,
что чем меньше
q,
тем быстрее сходимость. Вблизи корня
асимптотическая сходимость определяется
величиной
|
(![]() )|
и
будет особенно быстрой при
(
)|
и
будет особенно быстрой при
(![]() )
= 0.
Значит, успех метода зависит от того,
насколько удачно выбрано (x).
Например, для извлечения квадратного
корня, т.е. решения уравнения х2=а
можно положить (x)=
)
= 0.
Значит, успех метода зависит от того,
насколько удачно выбрано (x).
Например, для извлечения квадратного
корня, т.е. решения уравнения х2=а
можно положить (x)=
![]() или (x)
=
или (x)
=
![]() [x
+
[x
+
![]() ]
и соответственно написать такие
итерационные процессы:
]
и соответственно написать такие
итерационные процессы:
![]() или
или
![]() .
(4.5)
.
(4.5)
Первый
процесс вообще не сходится, а второй
сходится при любом
x0
>
0
и очень быстро, ибо
(![]() )=
0.
Второй процесс используют при извлечении
корня на клавишных машинах.
)=
0.
Второй процесс используют при извлечении
корня на клавишных машинах.
Каков
практический критерий сходимости, т.
е. когда надо прекращать итерации
(4.2)?
Из
(4.3)
видно, что если (![]() )
<
0,
то
итерации попеременно оказываются то
с одной, то с другой стороны корня
(рис
4.3, в,
г),
так что корень заключен в интервале
(хn,
хn+1).
Это
надежная, хотя несколько грубая оценка.
Но она не применима при
)
<
0,
то
итерации попеременно оказываются то
с одной, то с другой стороны корня
(рис
4.3, в,
г),
так что корень заключен в интервале
(хn,
хn+1).
Это
надежная, хотя несколько грубая оценка.
Но она не применима при
![]() >
0,
когда итерации сходятся к корню монотонно
(рис 4.3, а,
б),
т. е. с одной стороны.
>
0,
когда итерации сходятся к корню монотонно
(рис 4.3, а,
б),
т. е. с одной стороны.
Вблизи
корня итерации сходятся примерно как
геометрическая прогрессия со
знаменателем
q
=
 .
Чтобы
сумма дальнейших ее членов не превосходила
,
должен выполняться критерий сходимости:
.
Чтобы
сумма дальнейших ее членов не превосходила
,
должен выполняться критерий сходимости:
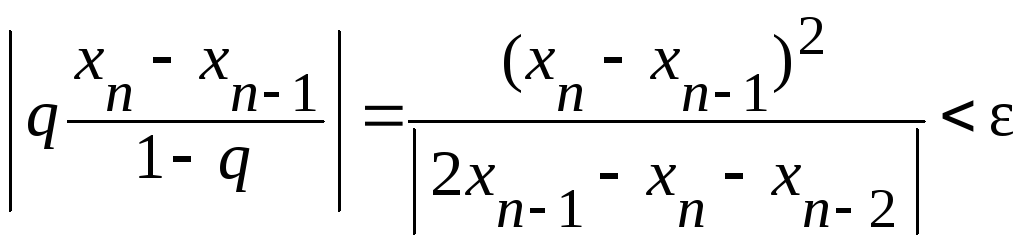 .
(4.6)
.
(4.6)










y











 y
y
q < 1 q > 1
x
x x
а
y






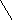






 q
< 1 y
q
> 1
q
< 1 y
q
> 1











 x 0
x2
x 2
x1
x
x2
x2
x1
x
x 0
x2
x 2
x1
x
x2
x2
x1
x
в г
Рис. 4.3. Графики функции, иллюстрирующие сходимость или расходимость: а, в – процедуры сходятся; б, г – расходятся
При выполнении этого условия итерации можно прекращать.
Метод простых итераций и почти все другие итерационные методы имеют важное достоинство: в них не накапливаются ошибки вычислений. Ошибка вычислений эквивалентна некоторому ухудшению очередного приближения. Но это отразится только на числе итераций, а не на точности окончательного результата. Подобные методы устойчивы даже по отношению к грубым ошибкам (сбоям ЭВМ), если только ошибка не выбрасывает очередное приближение за пределы области сходимости.
