
- •16. Основные понятия пуассоновского стационарного потока
- •17. Основные хар-ки пуассон. Стационарного потока
- •18. Моделирование процесса страхования автомобилей
- •19. Связь между дискретным марковским процессом с непрерывным временем и пуассоновским потоком
- •20. Моделирование процесса отказов банкоматов в операционном зале
- •21. Понятие сетевого проекта, работы и события
- •22. Резервы работ и событий сетевого проекта
- •23. Оптимизация сетевого проекта
- •24. Потоки в сетях и принцип их сохранения. Теорема Форда-Фалкерсона.
- •25. Построение максимального потока
- •30. Принципиальные системы регулирования товарных запасов. Саморегулирующиеся системы.
- •31. Модель экономически выгодных размеров заказываемых партий
- •26. Метод ветвей и границ
- •27. Классическая задача управления запасами
- •28. Принципиальные системы регулирования товарных запасов. Система с фиксированным размером заказа. Система с фиксированной периодичностью заказа
22. Резервы работ и событий сетевого проекта
Резервы событий и работ определяются следующими соотношениями:
- Резерв времени i-го событи: Ri=tni – tpi есть промежуток времени, на который может быть отсрочено наступление события без нарушения сроков завершения всего комплекса работ.
- Полный резерв времени работы (i,j): R1ij = tni – tpi - tij - максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы (i,j) без изменения общего срока выполнения комплекса работ.
- Свободный резерв времени работы: R2ij = tpi - t0i – tij - максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы (i,j)при условии, что все события сети наступят в свои сроки.
- Полный резерв времени пути: R(LП) = ТКР - ТП, где ТП – продолжительность пути LП , а ТКР – продолжительность критического пути, показывает, на сколько могут быть увеличены продолжительности всех работ в сумме пути LП относительно критич. пути LКР.
- Коэффициент
напряжённости работы (i,j)
kHij
=
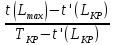 - характеризует напряжённость по срокам
выполнения работы (i,j)
. Здесь
- характеризует напряжённость по срокам
выполнения работы (i,j)
. Здесь
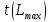 – длительность максимального из
некритических путей, проходящих через
работу (i,j),
– длительность максимального из
некритических путей, проходящих через
работу (i,j),
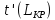 – продолжительность части критических
работ, входящих в рассматриваемый путь
– продолжительность части критических
работ, входящих в рассматриваемый путь
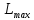 .
.
Чем ближе коэффициент напряжённости к 1, тем сложнее выполнять эту работу в установленные сроки.
Методы расчёта параметров сетевой модели делятся на 2 группы. В 1ю входят аналитические методы, которые включают вычисления по формулам непосредственно на сетевом графике, табличный и матричный методы. Ко 2й группе относятся методы, основанные на теории статистического моделирования, которые целесообразно применять при расчёте стохастических цепей с очень большим разбросом возможных сроков выполнения работ.
При малом (до 100) числе событий наиболее удобным является табличный метод расчёта параметров. Применение этого метода позволяет вычислить времена наступления событий (ранее и позднее), определить критический путь и критическое время выполнения всего комплекса работ, а также вычислить имеющиеся временные резервы. После определения параметров следует провести анализ и оптимизацию сетевого графика.
23. Оптимизация сетевого проекта
Анализ сетевой модели необходимо проводить с целью выявления резервов и «узких мест». Следует помнить, что обнаруженные резервы позволяют более гибко управлять комплексом работ путём их перераспределения с одних работ на другие по специальным методам оптимизации.
Т.к. не все работы критические, можно уменьшить Ткр за счёт резервов, перебросив их часть на критические работы, и тем самым получить новые сроки выполнения работ и соответственно меньшее Ткр.
Оптимальным сетевым планом будет план с минимальным Ткр0 в данных условиях. Очевидно, что новые длительности всех путей в таком случае будут равны, т.е. Ткр0=Тl0, l = 1,2,…
Механизм
перераспределения средств включает
уменьшение средств части работ (i,j)
на некоторую величину xij
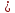 bij,
что приводит, естественно, к увеличению
времени её выполнения
bij,
что приводит, естественно, к увеличению
времени её выполнения
t’ij
= ʄ (xij)
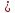 tij.
Средства Xij
, вложенные в другую работу (h,k),
xij=xhk,
приводят к уменьшению времени её
выполнения t’hk
= ʄ (xhk)
tij.
Средства Xij
, вложенные в другую работу (h,k),
xij=xhk,
приводят к уменьшению времени её
выполнения t’hk
= ʄ (xhk)
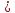 thk.
thk.
Продолжительность выполнения работ зависит от объёма выделенных ресурсов, работает формула «время – деньги» и не зависит от того, каким образом эти ресурсы были инвестированы. Эта зависимость нелинейная и может быть представлена выражением
t=t0
exp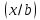 .
.
На приктике эти функции обычно линеализируют, представляя их приближенно в виде:
t’ij=tij
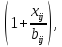 t’hk=thk
t’hk=thk
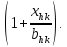
В связи с тем, что
выделенные ресурсы ограничены, должно
выполняться условие их сохранения, т.е.
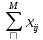 =
=
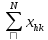 , где M
– число работ, с которых средства
снимались, а N
– число работ, на которые средства
переносились.
, где M
– число работ, с которых средства
снимались, а N
– число работ, на которые средства
переносились.
На этом основании общий срок выполнения всего комплекса работ определяется целевой функцией следующего вида:
Ткр
=
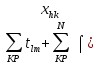 ),
где (l,m)
- номера работ критического пути,
средства которых не изменялись.
),
где (l,m)
- номера работ критического пути,
средства которых не изменялись.
В процессе
перераспределения средств необходимо
соблюдать условие ограничения на
величину снимаемых средств
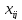 с работы (i,j)
, которое определяется наличием
свободного резерва времени R2ij
у этой работы, и определяется формулой:
с работы (i,j)
, которое определяется наличием
свободного резерва времени R2ij
у этой работы, и определяется формулой:
tij
+ R2ij
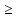 tij
tij
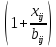 и, следовательно, удовлетворяет условию
xij
и, следовательно, удовлетворяет условию
xij
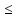
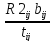 .
.
Решение задачи оптимизации состоит в последовательном переносе средств с некритических работ на критические, переходя от одного пути к другому до тех пор, пока все работы не будут критическими и не будут иметь резервов, а длительности всех путей станут равными. Следует отметить, что переносить средства с работы одного пути на любую работу, даже критическую, но входящую в этот же путь нельзя.
