Вопрос 2.
Логика рассмотрения вопроса об анализе влияния изменения факторов на изменение результативного показателя требует начинать с простейших случаев. Рассмотрим зависимость между объёмом продукции (q), производительностью труда (w) и объёмом трудовых затрат (Т).
q=w*T
В задачах такого типа связь между факторами и результативными факторами можно рассмотреть в причинно-следственном аспекте. В подобных случаях решаются и типовые задачи:
1)Оценка влияния относительного изменения факторов на относительное изменение результативного показателя.
2)Оценка влияния абсолютного изменения каждого фактора на абсолютное изменение результативного показателя.
3)Определение отношения величины прироста вызванного изменением каждого фактора к величине результативного п=оказателя за базисный период.
4)Определение доли абсолютного прироста, вызванное изменением каждого фактора к величине результативного показателя .
Все 4 типа задач рассмотрим на примерах:
Среднечасовая выработка измеряется Т/чел.-ч. – w
Общее количество отработанных рабочими чел.-ч. – Т
Объём произведённой продукции Т – q
1 задача:
q=w*T
2 задача:
Определим влияние абсолютного изменения каждого из факторов на общее абсолютное изменение результативного показателя
К
сожалению 
нельзя пренебречь, т.к. эта величина не
является бесконечно малой и с другой
стороны она не имеет никакого экономического
смысла.
Рассмотрим логарифмический метод разложения по факторам полного приращения результативного показателя:
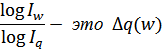
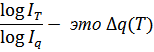
3 задача:
Сводится к вычитанию отношений
и 
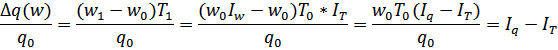
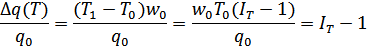
4 задача:
При решении речь пойдёт об отношении
и 
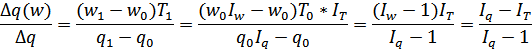
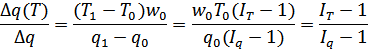
Вопрос 3.
Рассмотрим аддитивную модель:
Прибыль от реализации промышленной продукции – х1;
Прочая прибыль – х2;
Итого балансовая прибыль –у
В аддитивной модели: у=х1+х2
Сумма абсолютных приростов по факторам равна общему приросту результативного показателя △у=△х1+△х2
Определим удельный вес прироста полученного за счёт изменения каждого фактора в общем приросте результативного показателя
Темпы прироста результативного показателя определяются ростом х1 и х2.
Вопрос 4.
Проблемы, возникающие при анализе влияния изменения многих факторов на изменение результативного показателя схожими с возникающими при рассмотрении двух факторных моделей:
у-результативный показатель
хi-факторы
n- число включённых в модель факторов
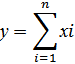
Арифметическое разложение по факторам
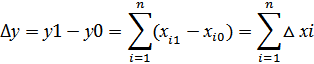
Анализировать подобную многофакторную модель можно по аналогии с 2-хфакторной. Большинство многофакторных мультипликативных моделей строится по единому принципу путём разложения детализации как фактора в исходной 2-хфакторной модели.
Пример: Объём продукции равен уровню производительности труда умноженному на массу трудовых затрат.
Производительность труда равна средней часовой выработке умноженной на среднюю продолжительность рабочего дня.
Следовательно у=х1*х2*х3
Рассмотрим анализ многофакторной мультипликативной модели: у=а*b*c
1)Относительная форма анализа влияния изменения факторов на изменение результативного показателя
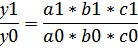
2)Абсолютное изменение результативного показателя
△у = (а0+△а)(b0+△b)(c0+△c) - a0*b0*c0 = a0*b0*c0 + a0*△b*c0 +△a*b0*c0+△a*△b*c0+ a0*b0*△c + a0*△b*△c+ △a*b0*△c+ △a*△b*△c - a0*b0*c0 = △a*b0*c0 + △b*a0*c0 + △c*a0*b0 + △a*△b*c0 + a0*△b*△c + △a*△c*b0 + △a*△b*△c
не имеет экономического смысла
Следовательно △у=△a*b0*c0+а1△bc0+a1b1△c