2. Определение положения нейтральной оси при косом изгибе. Расчеты на прочность.

Нейтральная ось – линия, во всех точках которой нормальные напряжения равны нулю. При этом в точках сечения, наиболее удаленных от нейтральной оси нормальные напряжения принимают свои экстремальные значения – минимум и максимум.

Выведем формулу для определения положения нейтральной оси при косом изгибе.

Так как =0, то можем записать:

Отсюда найдем уравнение нейтральной оси:

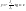
Более удобно записать это уравнение через угол β наклона нейтральной линии к оси Oz:

Знак «минус» в этой формуле показывает, что углы α и β откладываются от разноименных осей, но в одном направлении.

Как видим, в случае, когда J_z ≠ J_y, углы α и β не равны друг другу, а, значит, и плоскость кривизны (плоскость максимальных прогибов) бруса не будет совпадать с плоскостью действия сил. Поэтому такой изгиб и назван «косым».

Определим максимальные нормальные напряжения при косом изгибе и запишем условие прочности.

Как известно, нормальные напряжения достигают своих экстремальных значений в точках, наиболее удаленных от нейтральной оси (координаты таких точек обозначим y_уд. и z_уд.). Стало быть, можем записать:

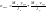
или

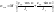
Для прямоугольного сечения – это точки A и B. При M>0

В случае косого изгиба, как правило, проверка прочности осуществляется лишь по нор-мальным напряжениям (действие касательных невелико). Поэтому условие прочности запишем в виде: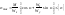

5.Определение критических напряжений. Пределы применения формулы Эйлера.

Вывод формулы Эйлера основан на применении дифференциального уравнения упругой линии. Поэтому воспользоваться этой формулой можно лишь в том случае, если справедлив закон Гука, т. е. пока критическое напряжение (напряжение сжатия, соответствующее критической силе) не превышает предела пропорциональности:

Действительно, если прямолинейная форма стержня остается устойчивой и при напряжениях, превышающих предел пропорциональности, то дифференциальное уравнение (14.3), предполагающее справедливость закона Гука, уже непригодно.

Выведем формулу для критического напряжения

Введя безразмерную величину

называемую гибкостью стержня, окончательно получим

Формула Эйлера становится непригодной при гибкости стержня, меньшей предельного значения , зависящего только от свойств материала.

15. Неразрезные балки. Вывод уравнения трех моментов.

Неразрезные балки – это балки, которые лежат на нескольких опорах и на своем протяжении не имеют ни разрывов ни шарниров. Обычно одна одна опора шарнирно неподвижная(или защемление), а остальные опоры шарнирно-подвижные.

Уравнение трех моментов представляет собой соотношение между изгибающими моментами в трех последовательных опорах одной неразрезной балки. Например, в случае неразрезной балки с равномерной нагрузкой на каждом пролете это уравнение имеет вид

M_AL₁ + 2M_B (L₁ + L₂) + M_CL₂ = – (W₁L₁³)/4 – (W₂L₂³)/4.