
- •Обработка статистической информации о надежности исследуемого объекта
- •Упорядочение исходной выборки наработок до отказа
- •Проверка статистических гипотез
- •Проверка статистической гипотезы о соответствии экспоненциальному распределению
- •Проверка статистической гипотезы о ее соответствии распределению Вейбулла
- •Проверка статистической гипотезы о соответствии выборки нормальному или логарифмически нормальному распределению
- •Оценивание параметров распределений
- •Аналитические методы получения точечных оценок
- •Графическое оценивание параметров распределений
- •Оценивание показателей безотказности
- •Восстановление работоспособного состояния
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Магнитогорский государственный технический университет им. Г. И. Носова
Кафедра: МОМЗ им. 50летия МГМИ
КУРСОВАЯ РАБОТА
по дисциплине «Надежность, эксплуатация и
техническое обслуживание металлургических машин».
Обработка статистической информации о надежности
линии привода 3-го формирующего ролика 1-й моталки
Разработал: ст.гр.КММа-10
Зырянов А.С.
Проверил: профессор.
Жиркин Ю.В.
Магнитогорск
2010
Содержание:
Обработка статистической информации о надежности
исследуемого объекта…………………………………………………………………...……….3
-
Упорядочение исходной выборки наработок до отказа……………………………….3
-
Проверка статистических гипотез………………………………………………………5
-
Проверка статистической гипотезы о соответствии
-
экспоненциальному распределению……………………………………………….5
-
Проверка статистической гипотезы о ее соответствии распределению
Вейбулла……………………………………………………………………………..7
-
Проверка статистической гипотезы о соответствии нормальному или
логарифмически нормальному распределению…..................................................8
-
Оценивание параметров распределений……………………………………………….9
-
Аналитические методы получения точечных оценок…………………………….9
-
Графическое оценивание параметров распределений…………………………..11
-
-
Оценивание показателей безотказности………………………………………………14
-
Восстановление работоспособного состояния………………………………………..16
Литература………………………………………………………………………………………18
Приложение……………………………………………………………………………………..19
Обработка статистической информации о надежности исследуемого объекта
Первое, что необходимо иметь - это документ, в котором зарегистрированы моменты отказов оборудования. Виды таких документов рассмотрены в первой главе пособия.
Такой документ будем называть первичной статистической совокупностью. Рассмотрение и осмысление такого документа затруднительно с целью представить себе характер распределения.
Первый шаг к осмыслению материала - это его упорядочение, расположение в порядке возрастания значений наработок. Полученный ряд будем называть упорядоченной статистической совокупностью. По упорядоченной статистической совокупности уже можно построить статистическую функцию распределения.
Характерной особенностью работ при проведении испытаний на надежность в процессе эксплуатации изделий является повышенная опасность грубых ошибок. Для статистической информации о надежности сравнительна высока вероятность попадания в выборку аномальных реализаций либо как результат ошибки, например в фиксации момента отказа, либо как результат ошибки при классификации отказов.
Исходные данные:
Вариант №4
Линия привода 3-го формирующего ролика 1-й моталки.
Наработки, сут.: 14,8,8,7,9,36,75,41,70,48,22,15,18,8,23,57.
-
Упорядочение исходной выборки наработок до отказа
Упорядочим исходную выборку:
7,8,8,8,9,14,15,18,22,23,36,41,48,57,70,75
N=16 шт.
Проверка принадлежности необычайно
малой или большой наработки к исходной
выборке может быть осуществлена с
помощью F-распределения
для заданного уровня значимости
![]() и
фактического числа наработок (табл.1
прил.) [1]
и
фактического числа наработок (табл.1
прил.) [1]
Если выполняется равенство
 (1.1)
(1.1)
то наработка необычно малая и не должна приниматься во внимание.
Если выполняется равенство
 (1.2)
(1.2)
то наработка необычно большая и ее следует отбросить,
где r – число наработок до отказа;
tmin – минимальное значение наработки;
tmax – максимальное значение наработки.
Процентили F-распределения находятся из табл. 1 прил. [1]
В соответствии с формулой (1.1) находим:

![]()
Из табл. 1 прил. для
![]() =0,05
=0,05
![]()
Следовательно, наработка до отказа t1 = 7 сут. не является необычно малой и ее нельзя исключать из выборки.
По формуле (1.2) находим:

![]()
По табл. 1 прил. для
![]() =0,05
[1]
=0,05
[1]
![]()
Вывод – наработка t = 75 сут. не является необычно большой и ее нельзя исключать из выборки.
-
Проверка статистических гипотез
-
Проверка статистической гипотезы о соответствии экспоненциальному распределению
-
Для проверки статистической гипотезы наиболее мощным является критерий Бартлетта:
 ,
(2.1)
,
(2.1)
где
![]() -
оценка средней наработки до отказа;
-
оценка средней наработки до отказа;
r – число наработок до отказа;
ti – значение i-той наработки.
Все вычисления сведем в таблицу:
Таблица 1
|
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
|
|
7 |
8 |
8 |
8 |
9 |
14 |
15 |
18 |
22 |
23 |
36 |
41 |
48 |
57 |
70 |
75 |
28,7 |
--- |
|
|
2 |
2,1 |
2,1 |
2,1 |
2,2 |
2,6 |
2,7 |
2,9 |
3,1 |
3,2 |
3,6 |
3,7 |
3,9 |
4 |
4,2 |
4,3 |
--- |
48,6 |

![]()
Выполняется условие:
![]() ;
;
где
![]() для заданного уровня значимости
для заданного уровня значимости
![]() ,
числа отказов r находится
из табл. 5 прил., следовательно гипотеза
о принадлежности выборки к экспоненциальному
распределению не отвергается.
,
числа отказов r находится
из табл. 5 прил., следовательно гипотеза
о принадлежности выборки к экспоненциальному
распределению не отвергается.
Проверку можно осуществить и с помошью критерия Пирсона:
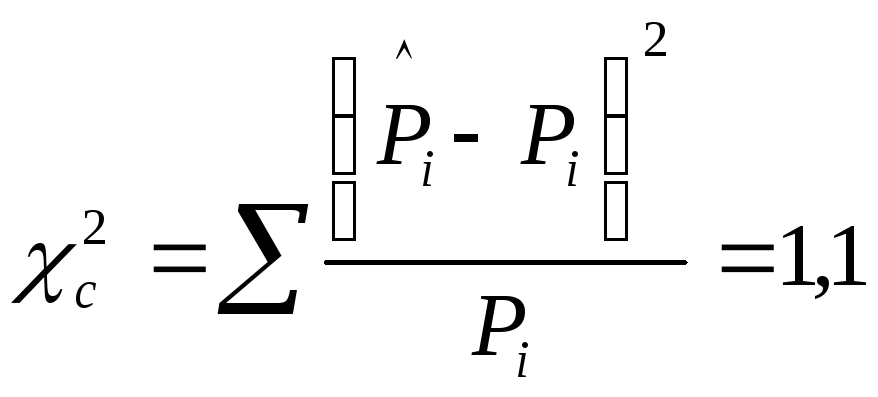 ,
(2.2)
,
(2.2)
где
![]() -
теоретическая частота,
-
теоретическая частота,
![]() -
число интервалов.
-
число интервалов.
Все вычисления сведем в таблицу:
Таблица 2
|
|
1-12 |
12-24 |
24-36 |
36-48 |
48-60 |
60-75 |
|
|
|
5 |
5 |
1 |
2 |
1 |
2 |
|
|
|
0.31 |
0,31 |
0,0625 |
0,125 |
0,0625 |
0,125 |
|
|
|
0.14 |
0,14 |
0,06 |
0,0077 |
0,06 |
0,0077 |
0,425 |
Число интервалов -
![]() .
.
Протяженность интервалов -
![]() .
.
Теоретическая частота -
![]()
Для
![]() и к-2=6-2=4 по табл.5 прил. находим -
и к-2=6-2=4 по табл.5 прил. находим -
![]()
Так как соблюдается неравенство:
![]() ,
,
то гипотеза о принадлежности выборки к генеральной совокупности, описываемой экспоненциальным распределением, не отвергается.

