Двойной интеграл
№№ 97 – 100. Изменить порядок интегрирования в следующих интегралах
97.
. 98.
.
99.
. 100.
.
№№ 101 – 104. Перейти к полярным координатам и вычислить интегралы
101.
,
где
.
102.
.
103.
.
104.
,
где
.
№№ 105 – 108. Вычислить следующие интегралы
105.
,
где
.
106.
,
где
.
107.
,
где
.
108.
,
где
- фигура, ограниченная линиями
,
,
.
№№ 109 – 112. С помощью двойного интеграла найти площади фигур, ограниченных указанными линиями
109.
.110. 
.
111.
.
112.
.
113.
Найти статический момент однородного
полукольца, расположенного между
окружностями радиусов
и
относительно основания полукольца.
114.
Найти координаты центра масс однородного
кругового сектора, соответствующего
центральному углу
.
115.
В каком отношении гиперболоид
разделит объем шара
?
116.
Вычислить момент инерции сегмента,
отсекаемого от параболы
прямой
,
относительно прямой
.
№№ 117 – 120. Найти объемы тел, ограниченных следующими поверхностями
117.
.
118.
.
119.
.
120.
.
Тройной интеграл
№№ 121 – 124. Перейти к цилиндрическим координатам и вычислить следующие интегралы
121.
,
где область
ограничена поверхностями
.
122.
.
123.
.
124.
,
где область
ограничена поверхностями
.
№№ 125 – 128. Перейти к сферическим координатам и вычислить следующие интегралы
125.
,
.
126.
,
где область
ограничена поверхностями
и
.
127.
.
128.
,
где
.
№№ 129 – 134. Найти объем тел, ограниченных поверхностями
129.
,
,
,
.
130.
,
,
.
131.
,
,
.
132.
,
,
.
133.
,
,
.
134.
,
.
135.
В каком отношении поверхность
разделит объем шара
?
136.
С какой силой притягивает однородный
шар
массы
материальная точка
массы
?
137.
Определить момент инерции однородного
цилиндра
плотности
относительно прямой
.
138.
Найти массу тетраэдра, ограниченного
плоскостями
,
плотность которого меняется по закону
.
Несобственные интегралы
139.
Можно ли подобрать такое
,
чтобы
сходился?
140.
Функция
непрерывна на
и
.
Может ли сходиться
?
141.
Если
сходится, то обязательно ли
?
142.
Найти v.p.
.
143.
При каких
сходится интеграл
?
№№ 144 – 151. Исследовать сходимость несобственных интегралов
144.
. 145.
.
146.
. 147.
.
148.
. 149.
.
150.
. 151.
.
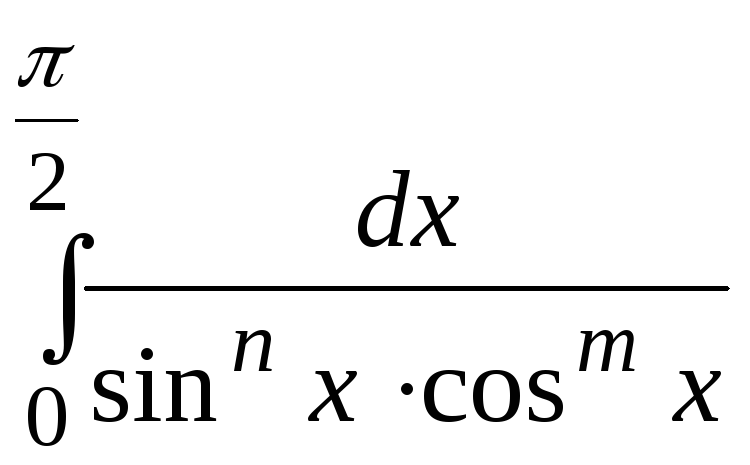Интегралы, зависящие от параметра
152.
Доказать, что функция
удовлетворяет
уравнению
.
153.Доказать,
что функция
удовлетворяет уравнению
.
154.
Доказать непрерывность функции
.
155.
Исследовать на непрерывность функцию
при
.
№№ 156 – 159. Исследовать несобственные интегралы, зависящие от параметра, на равномерную сходимость в указанных интервалах
156.
,
. 157.
,
.
158.
,
. 159.
,
.
№№ 160 – 165. Вычислить интегралы с помощью дифференцирования либо интегрирования по параметру
160.
.
161.
,
.
162.
. 163.
,
.
164.
,
. 165.
,
.
№№ 166 – 171. Вычислить с помощью эйлеровых интегралов
166.
. 167.
.
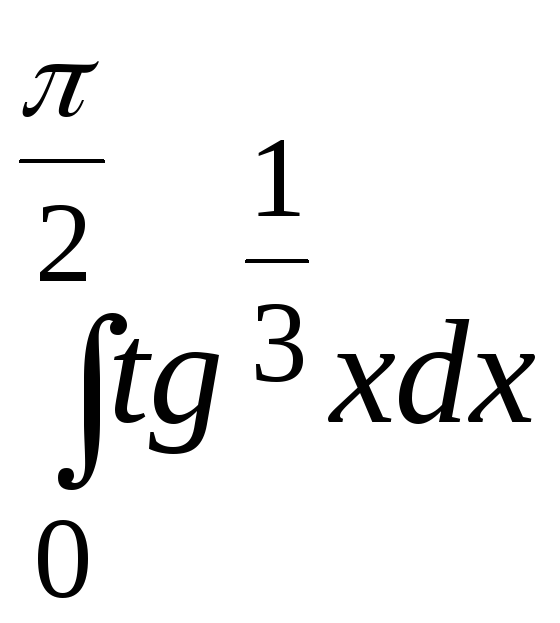168.
. 169.
.
170.
. 171.
,
.