1.7. Ряды Фурье

Функциональный ряд вида

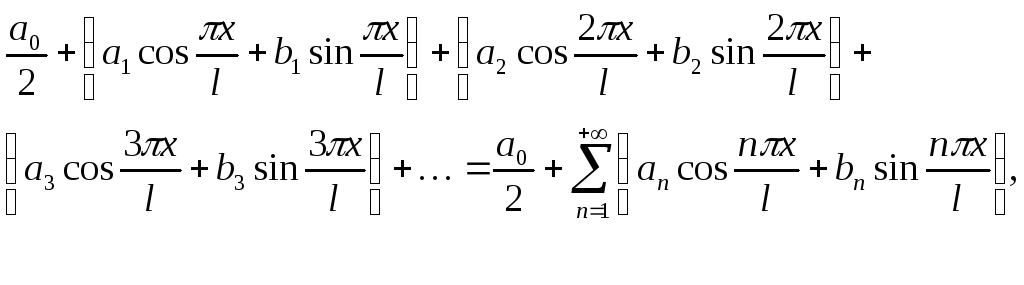(1)

где— постоянные, называется триго­нометрическим рядом.

Все члены тригонометрического ряда — синусы и косинусы уг­лов, кратных и их сумма S (х), если она существует, являются

периодическими функциями от с периодом . Поэтому тригонометрические ряды широко применяются для изу­чения различных периодических процессов в электротехнике, радио­технике, в теории упругих механических колебаний и во многих других областях естествознания и техники.

Разложение данной функции в тригонометрический ряд назы­вается гармоническим анализом, ибо этим достигает­ся разложение какого-либо сложного периодического явления на простые гармонические колебания.

Рядом Фурье для функции в интервале называется тригонометрический ряд вида (1), если его коэффициенты и вычислены по формулам Фурье:

(2)

I

Простейшие достаточные условия разложимости функции в ряд Фурье сформулированы в следующей теореме Дирихле.

Если в интервале функция имеет конечное число то­чек разрыва первого рода (или непрерывна) и конечное число точек экстремума (или не имеет их вовсе), то ее ряд Фурье сходится, т. е. имеет сумму во всех точках этого интервала. При этом:

а) в точках непрерывности функции он сходится к самой функ­ции,

б) в каждой точке разрыва функции — к полусумме односто­ронних пределов функции слева и справа,

в) в обеих граничных точках интервала— к полусумме односторонних пределов функции при стремлении х к этим точкам изнутри интервала,

Для четной функции все коэффициенты и соответствующий ряд Фурье не содержит си­нусов

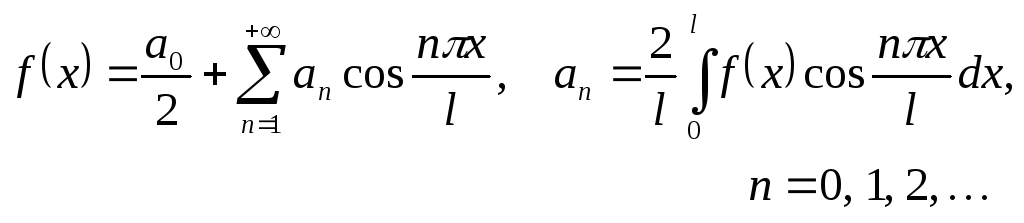(3)

Для нечетной функции все коэффициенты и соответствующий ряд Фурье содер­жит только синусы

(4)

Если функция, удовлетворяющая условиям теоремы Дирих­ле, является периодической, то на всей числовой оси ее ряд Фурье в точках непрерывности функции сходится к самой функции, а в каждой точке разрыва функции — к полусумме ее односторон­них пределов.

Функцию, заданную в интервале можно произволь­но продолжить в соседний интервал и поэтому ее можно представить различными рядами Фурье. Пользуясь этим, такую функцию обычно представляют неполным рядом Фурье, содержа­щим только косинусы или только синусы.

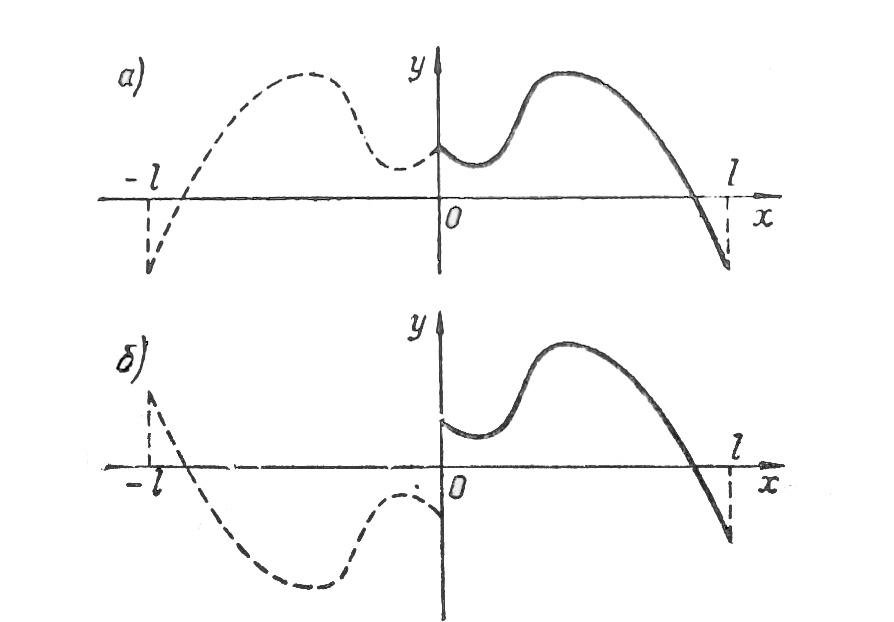
Ряд по косинусам получается при четном, а ряд по синусам при нечетном продолжении данной функции на соседний слева интер­вал В первом случае график данной функции продолжает­ся на интервал симметрично относительно оси ординат, а во втором случае — симметрично относительно начала координат.

С помощью формул Эйлера получается удобная во мно­гих случаях комплексная форма ряда Фурье:

где (5)

Если функция задана несколькими различными формулами на разных частях интервала , то при разложении ее в ряд Фурье, при вычислении интегралов в формулах (2) или (5) для ко­эффициентов ряда, следует разбить интервал интегрирования точ­ками, в которых меняется аналитическое выражение функции, на части и затем вычислять указанные интегралы как сумму интегра­лов по составляющим частям.

При разложении функции в ряд Фурье в интервале пределы интегралов в формулах (2) или (5) будут и, а в случае произвольного интервала длины эти пределы будут и

Пример 1. Разложить в ряд Фурье данную функцию в указанном ин­тервале:

1)

2)

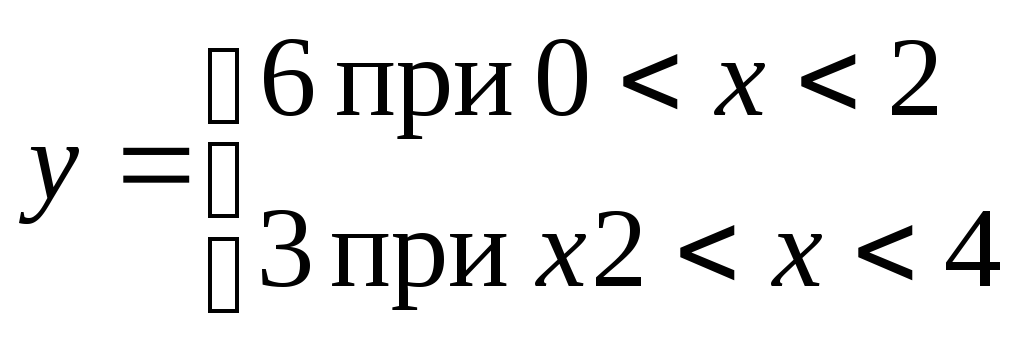
3)

4) Пользуясь полученным разложением, найти сумму ряда

Решение. Вначале проверяем, что данная функция в ука­занном интервале удовлетворяет условиям Дирихле; затем вычис­ляем коэффициенты и (или) по формулам Фурье и, подстав­ляя их в ряд (1) или (5)1, получаем искомое разложение данной функции в ряд Фурье; наконец, основываясь на теореме Дирихле, определяем, при каких значениях полученный ряд сходится к дан­ной функции.

1) Данная функция не четная и не нечетная, поэтому вычисляем ее коэффициенты Фурье по общим формулам (2), полагая и беря пределами интегралов 0 и, поскольку функция задана в интервале (0,):

(Для вычисления интеграла применена формула интегрирования по частям.)

При при полученное здесь выражение для не имеет смысла. Поэтому коэффициент вычисляем отдельно по формуле (2), полагая

Подставляя значения коэффициентов и в тригонометричес­кий ряд (1), получим искомое разложение данной функции в ряд Фурье:

Это разложение справедливо, т. е. полученный ряд сходится к данной функции во всех точках ее области определения

(В граничных точках и сумма ряда равна — в этих точках все члены ряда, кроме первого, обращаются в нуль. То же значение имеет сумма ряда в указанных точках и по теореме Дирихле.)

2) Пользуясь формулами (2), полагая и разбивая интер­вал интегрирования (0; 4) точкой на две части, поскольку в каждой из них функция задана различными формулами, получим:

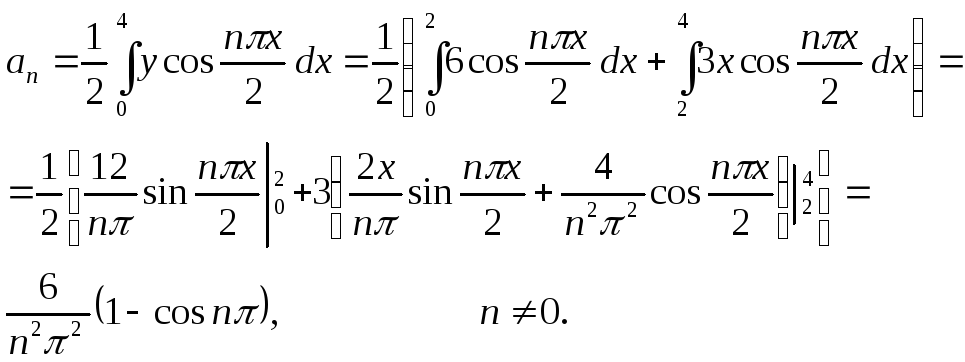
При четном и ; при нечетном

и

При по формуле (2) получим:

;

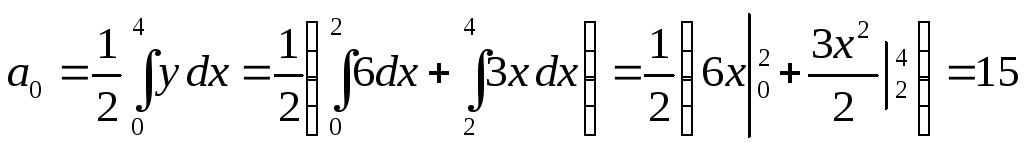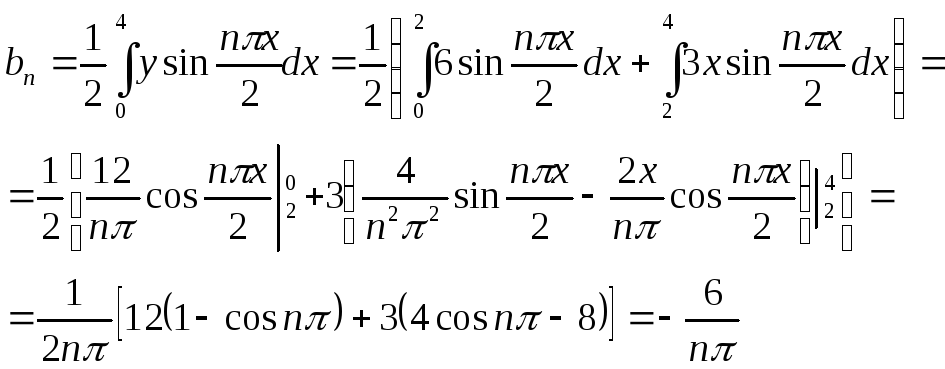
Искомое разложение данной функции имеет вид

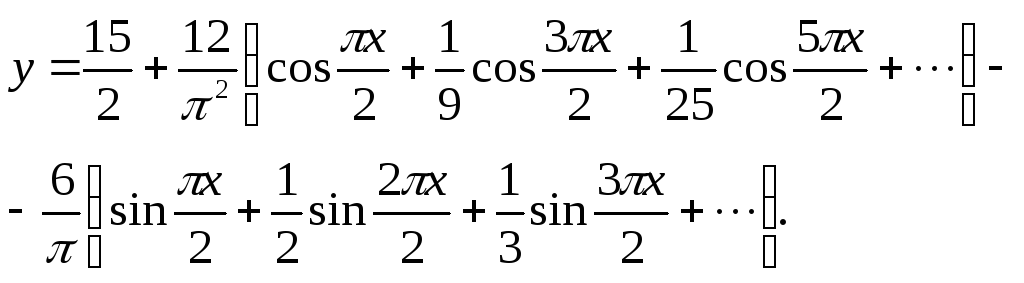
Оно справедливо во всей области определения данной функции: в интервале (0; 2) сумма рядаа в интервале (2; 4). В точке разрыва, где функция не определена,

,

2. Здесь удобно использовать комплексную форму ряда Фурье. По формуле (5):

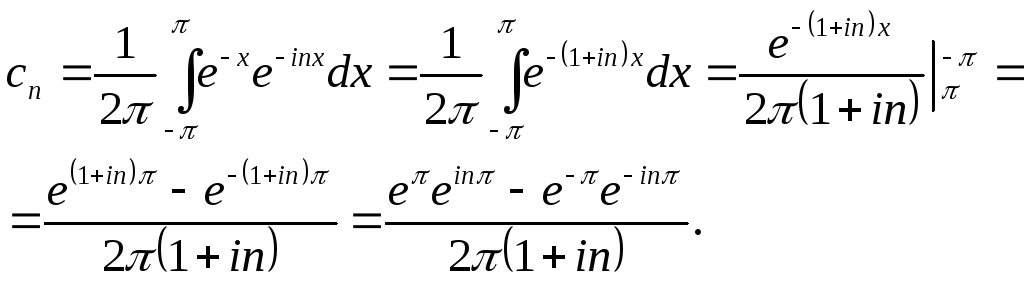
По формулам Эйлера

Следовательно,

В интервале ряд представляет функцию а в точках его сумма равна

Чтобы преобразовать полученный ряд в комплексной форме к обычной тригонометрической форме ряда Фурье (если это нужно), следует объединить слагаемые с индексами и и заменить в результате по формулам Эйлера показательные функции три­гонометрическими:

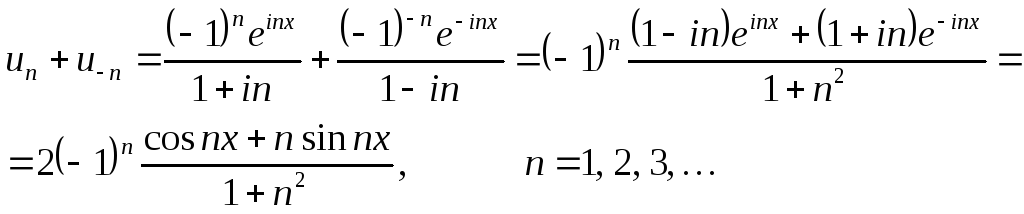
Из равенства, полагая , вычисляем

Следовательно,

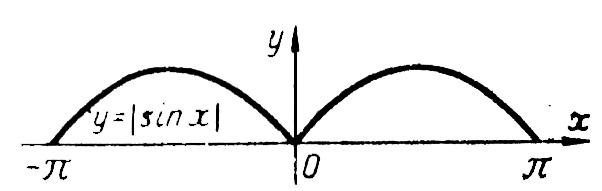
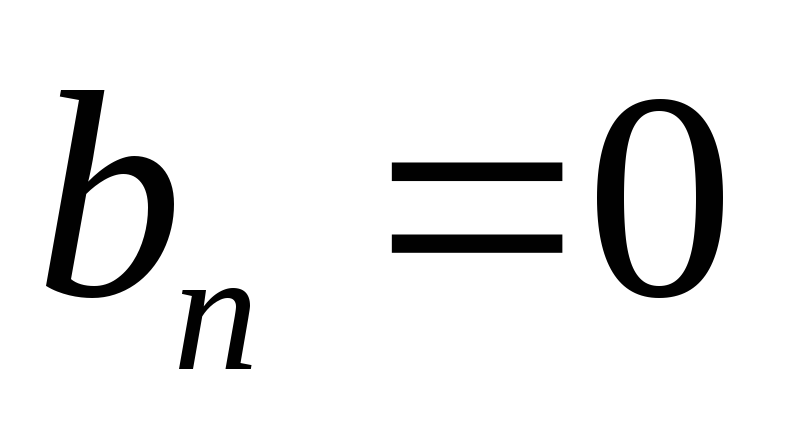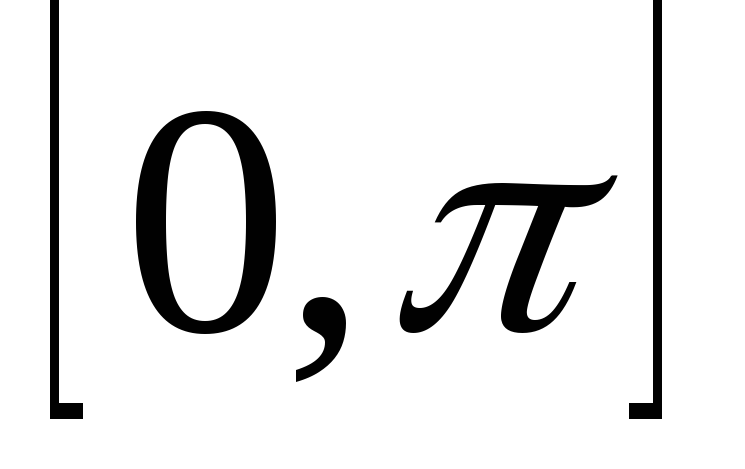2. Данная функция четная (черт. 202), вследствие чего все ко­эффициенты . В интервале функция определяется фор­муллой 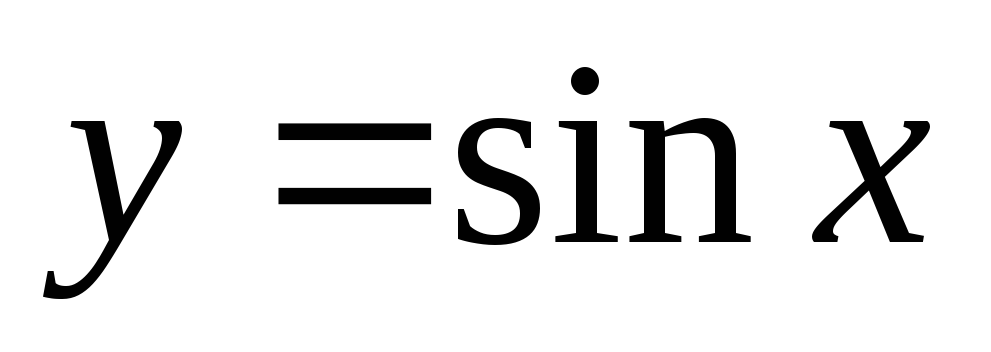. Поэтому по формуле (3), при 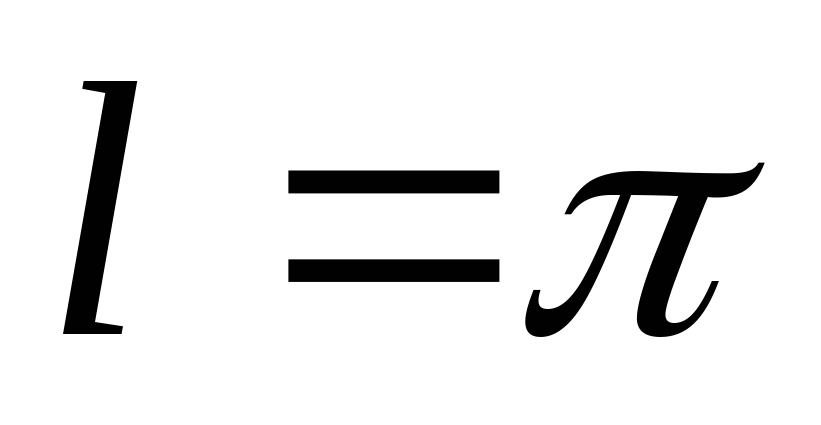, получим:

Если четное, , то и

Если нечетное, , то

При полученное здесь общее выражение для не пригод­но, вследствие чего коэффициент вычисляем отдельно, полагая, в формуле (2):

Подставив значения коэффициентов в ряд (1), получим искомое разложение

которое справедливо во всей области определения данной функции

·

При полученное разложение преобразуется в равенство

откуда и определяется сумма числового ряда, указанного в условии:

Здесь, как и в решении задач 1040 (1, 2), оказалось, что для дан­ной функции один из коэффициентов ряда нельзя было вычислить по найденному его общему выра­жению. Поэтому при разложении данной функции в ряд Фурье, пос­ле нахождения общих выражений для коэффициентов а_п и Ь_п, следует проверять, будут ли они пригод- _{Ц( г 202}

ны при всех [указанных в форму- ^ч'^г"

лах (2)] значениях п. Для тех зна­чений п, при которых эти общие выражения теряют смысл, необхо­димо вычислять соответствующие коэффициенты отдельно, подстав­ляя эти исключительные значения п в общие формулы Фурье.

Пример 2. Разложить в ряд Фурье периодические функции:

1) при

Пользуясь полученным разложением, найти сумму ряда:

а) б)

2) при

3) при

Решение. Все заданные функции удовлетворяют условиям те­оремы Дирихле, что обеспечивает возможность их разложения в ряд Фурье.

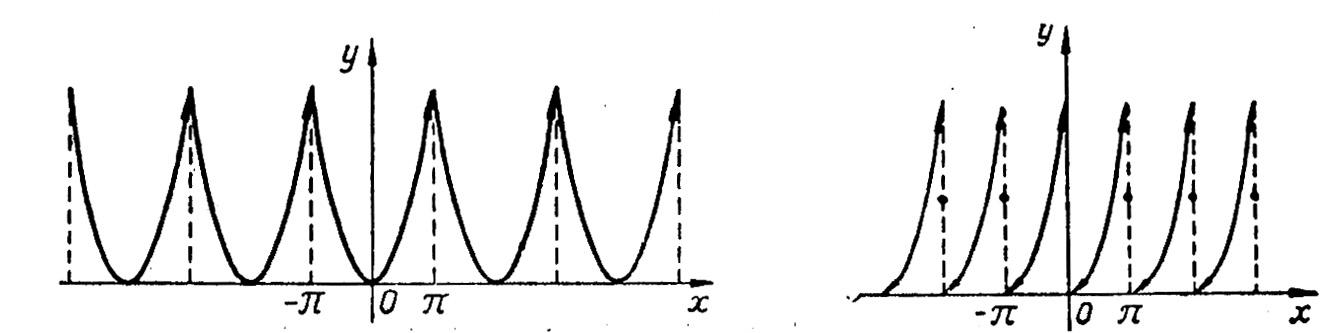
1) Данная функция четная, ее график (черт. 203) симметричен относительно оси. Все коэффициенты а коэффициенты вычисляются по формулам (3), при

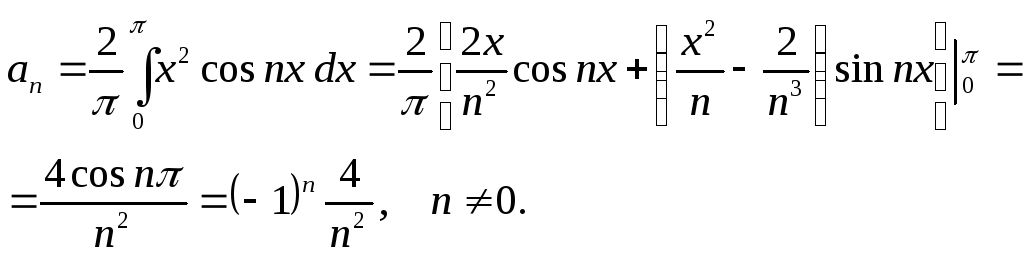
(Здесь дважды применена с}юрмула интегрирования по частям.) При (и) по формуле (3) найдем:

Следовательно,

Это разложение данной периодической и всюду непрерывной функции справедливо при любом значении, т. е. полученный ряд Фурье сходится к данной функции на всей числовой оси. Графики данной функции и суммы ее ряда Фурье полностью совпадают.

Полагая в полученном разложении найдем сумму ука­занного в условии числового ряда (а):

а полагая найдем сумму ряда (б):

1. Вычисляем коэффициенты Фурье данной функции по общим формулам (2), полагая (период этой функции равен, черт. 204):

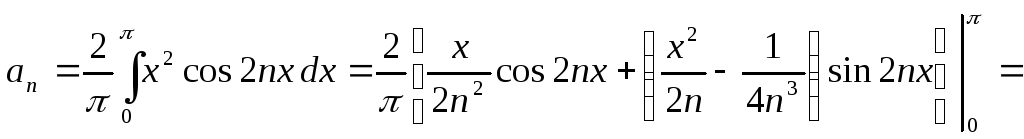
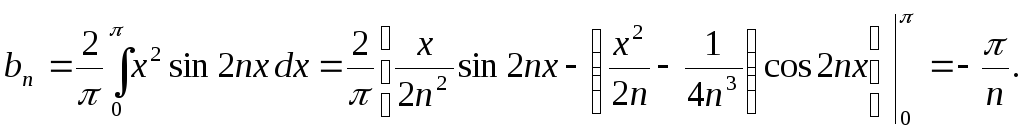
Подставляя найденные значения коэффициентов в ряд (1), по­лучим

.

Разложение справедливо во всей области определения данной периодической функции — на всей числовой оси, исключая точки, в которых функция разрывна (не определена). В точках разрыва функции полученный ряд также схо­дится. Согласно теореме Дирихле, в этих точках его сумма равна. У графика данной функции нет точек с абсциссами; график суммы ряда отличается от графика данной функции наличием точек .

3) Функция и нечетная. Поэтому коэффициенты , а вычисляем по формуле (4):

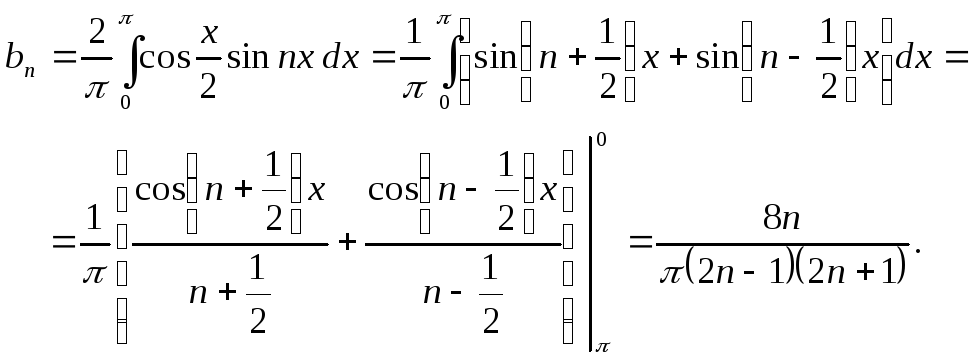
Следовательно,

П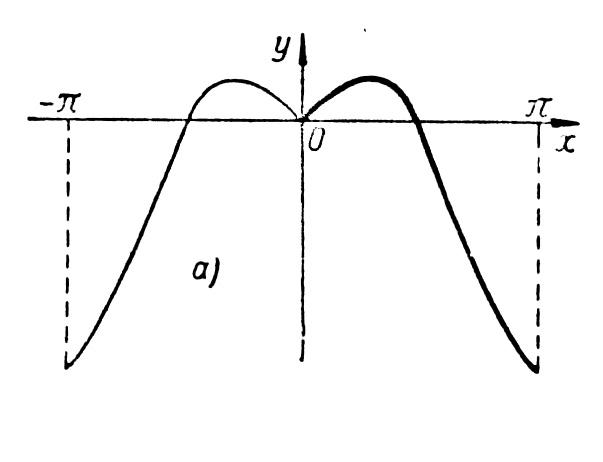олученное разложение данной функции справедливо во всей ее области непрерывности — при всех значениях, кроме значений, которые являются точками раз­рыва функции. В точках по теореме Дирихле сумма полученного ряда равна нулю. Это же очевидно потому, что в этих точках все члены ряда обращаются в нуль. Графики суммы ряда и данной функ­ции отличаются точками с абсциссами . У графика данной функ­ции ординаты этих точек равны –1, а у графика суммы ряда они равны 0.

Пример 3. Разложить данную функцию в указанном интервале в не­полные ряды Фурье, содержащие только косинусы или только си­нусы.

1. 

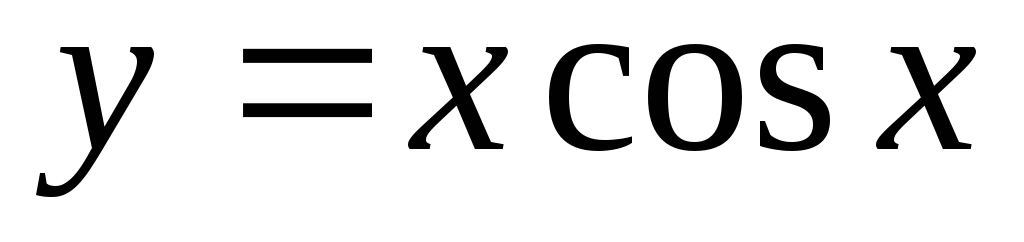2. в интервале от 0 до π. Пользуясь полученным разложением ряда .

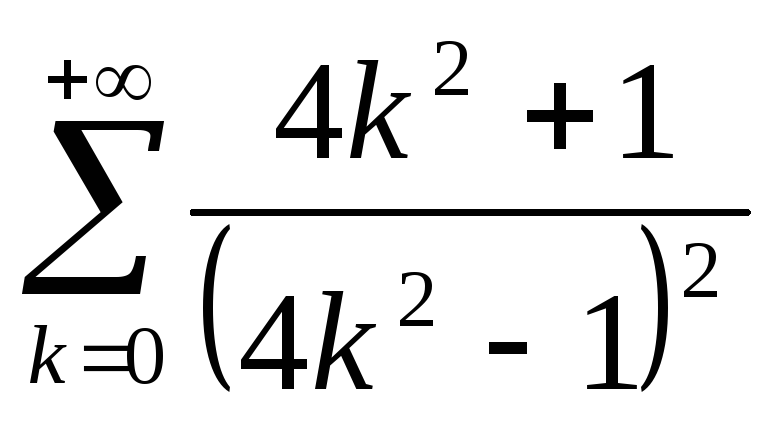Решение. 1) а. Чтобы получить разложение данной функции в ряд Фурье, содержащий только косинусы, продолжаем ее на со­седний слева интервал (— 1; 0] четным образом.

Тогда , а по формуле (3), подставляя, в интервале (0; 0,5) и в интервале (0,5; 1), найдем

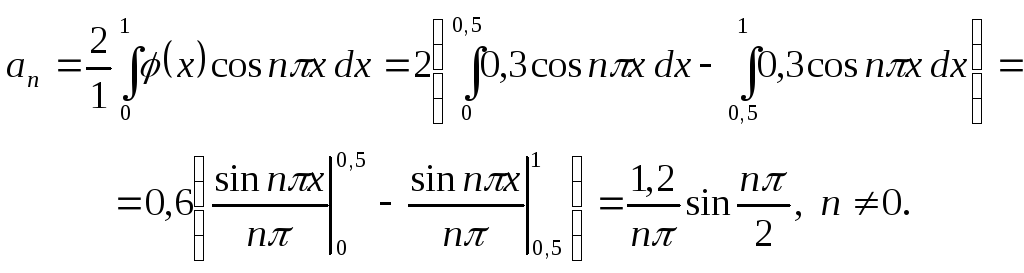
Если n четное, то .

Если n нечетное, , то

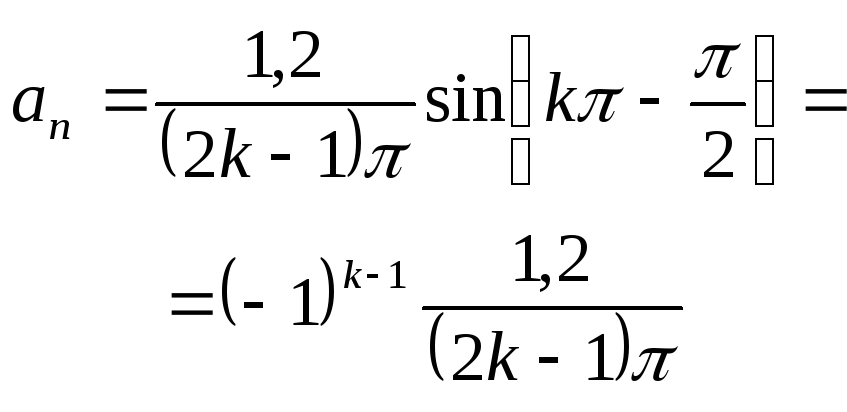
При по формуле (3) найдем

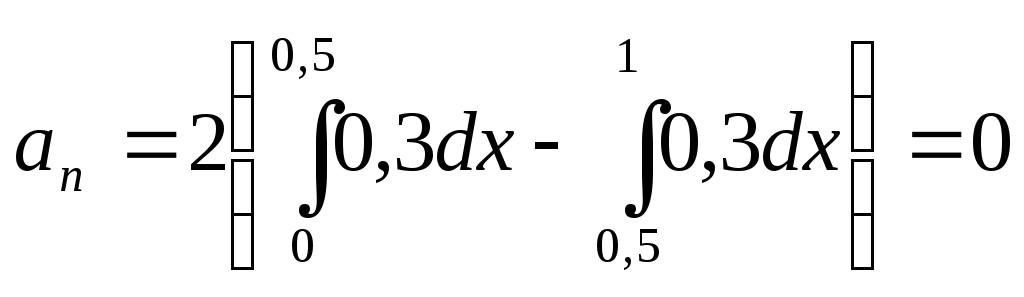
Следовательно, искомое разложение данной функции в непол­ный ряд Фурье, содержащий только косинусы, таково:

Оно справедливо во всей области определения данной функции. В интервале (0; 1) график суммы полученного ряда отличается от графика данной функции наличием точки (0,5; 0).

б. Для разложения данной функции в ряд Фурье, содержащий только синусы, продолжаем ее на соседний слева интервал (— 1; 0] нечетным образом .

Тогда , а по формуле (4)

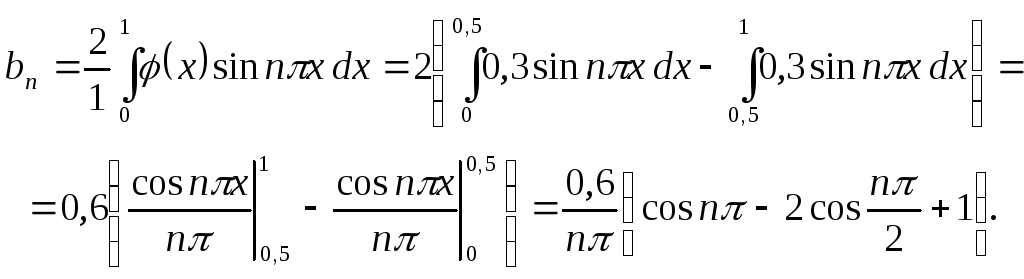
Если n нечетное, то .

Если n четное, , то

При четном k получим , при нечетном ,

, ,

Искомое разложение данной функции в неполный ряд Фурье, содержащий только синусы, имеет вид:

.

Оно справедливо во всей области определения функции .

2) а. Продолжив данную функцию четным образом, имеем: ,

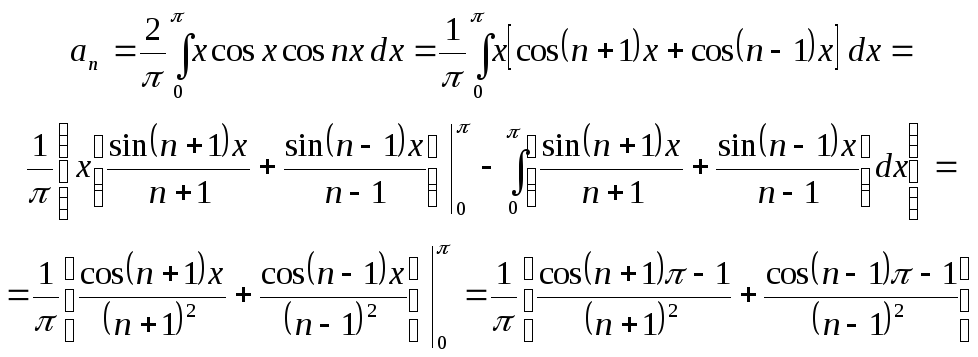
Если n четное , то и

.

Если n нечетное, то и .

Коэффициент вычислим отдельно, полагая в формуле (3):

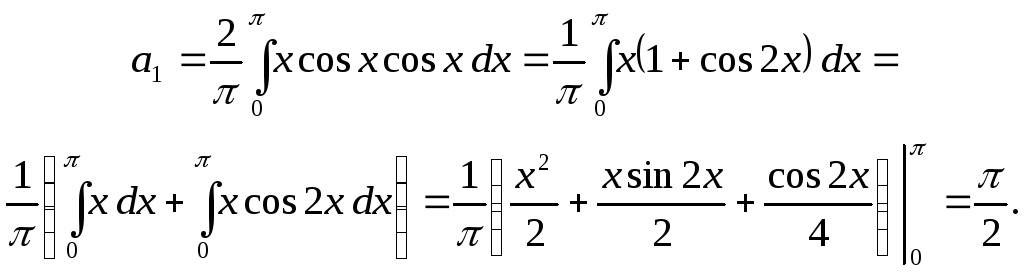
Таким образом, получаем следующее разложение данной функции в неполный ряд Фурье, содержащий только косинусы

Подставляя в полученное разложение, имеем:

, откуда следует

б. Продолжив данную функцию нечетным образом имеем ,

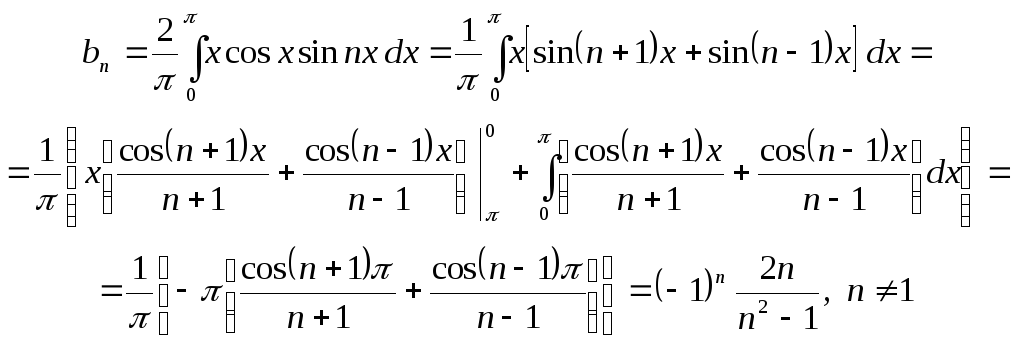
Коэффициент вычисляем отдельно:

.

Следовательно,