
- •Методические аспекты моделирования в асу и классификация моделей.
- •3. Организация статистического моделирования. Метод монте - карло.
- •Имитация равномерно распределенных случайных величин на интервале [0; 1].
- •Метод обратных функций. Примеры реализации.
- •Имитация векторных случайных величин; стандартный метод
- •Имитация нормально распределенных св (одномерный и многомерный случаи)
- •Анализ методов имитации случайных величин с заданным законом распределения (одномерный и многомерный случаи)
- •Имитация редких событий
- •Оценка количества реализаций, необходимых для достижения требуемой точности в методе статистических испытаний
- •Метод монте – карло и имитационное моделирование
- •Методы понижения дисперсии и методы вычисления интегралов
- •Регенеративный метод анализа моделей
- •Метод стратифицированной выборки
- •Методология имитационного моделирования
- •3. Формулировка математической модели.
- •Типовые математические схемы сложных систем. Агрегат и его функционирование,
- •4.Пример представления смо в виде агрегата.
- •7.Системная динамика
- •17.Метод лемера и сдвиг бернулли. Детерминированный хаос
- •35.Особенности моделирования организационно – экономических систем. Активные системы.
- •23.Характеристики интегрированной среды моделирования gpss
- •23.Основы моделирования в системе gpss
- •31.Смо; классификация и решение задач с помощью имитационного моделирования
- •36.Имитационное моделирование систем управления запасами
- •6.Метод Бокса-Уилсона.
- •3. Определение запаса для движения в направлении крутого восхождения
- •7. Проводим пошаговое приращение в каждом последующем опыте величины уровня фактора, учитывая знаки коэффициентов регрессии.
- •9. Классификация случайных процессов и корреляционные функции.
- •Корреляционные функции
- •18.Имитация потоков событий и случайных векторных величин.
- •19.Понятие детерминированного хаоса и показатель Ляпунова.
- •21. Особенности моделирования организационно-экономических систем. Производственные функции.
- •27.Системы массового обслуживания; классификация и решение задач аналитическим методом.
- •28.Методы имитации дискретных случайных величин.
- •30.Задача определения давления в пласте с помощью метода Монте-Карло.
- •32. Моделирование геологического разреза.
- •Теоретическая часть. Построение имитационной модели геологического разреза
- •34.Системы управления запасами; типовые математические модели.
- •37.Агентное моделирование.
- •Причины возникновения
- •Постановка задачи
- •Реализации
- •38.Имитация экспоненциально распределенных случайных величин.
- •40.Метод композиций; имитация св, подчиненных распределению хи квадрат.
-
Имитация равномерно распределенных случайных величин на интервале [0; 1].
Построение имитационных моделей требует использования случайных величин с заданным законом распределения. Особое место занимает случайная величина, имеющая равномерное распределения на отрезке [0, 1]. Во-первых, на ее основе можно получить величину, имеющею любой заданный закон распределения. Во-вторых, диапазон изменения такой величины совпадает с возможными значениями вероятности. В-третьих, множество чисел, заключенных между 0 и 1, несчетно и бесконечно, и никакой перечень действительных чисел из заданного интервала не исчерпает этого множества. И, наконец, имеется компактный и быстрый алгоритм имитации такой величины.
Пусть - непрерывная с.в., имеющая равномерное распределение на интервале (a, b). Тогда:
F(X)-ф-я
распределения f(X)-ф-я
плотности

Определим числовые характеристики с.в. , принимающей значения x:
Ч астный
случай ( a =0, b=1):
астный
случай ( a =0, b=1):

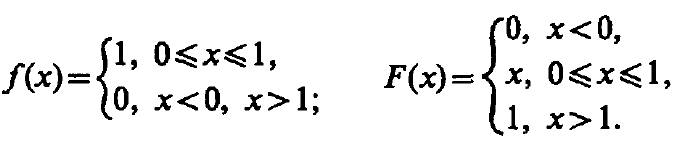
Такое распределение имеет м.о. M[] = 0.5; D[] = 1/12.
Это распределение требуется получить на ЭВМ. Но получить его на цифровой ЭВМ невозможно, так как машина оперирует с n – разрядными числами. Поэтому на ЭВМ вместо непрерывной совокупности равномерных случайных чисел интервала (0,1) используют дискретную последовательность 2n-случайных чисел того же интервала. Закон распределения такой дискретной последовательности называют квазиравномерным распределением.
На практике используют 3 основных способа генерации случайных чисел: аппаратный (физический), табличный (файловый), алгоритмический (программный) – наиболее рационален. К последним относится МЕТОД ВЫЧЕТОВ (метод Лемера или конгруэнтный метод) - один из основных методов, используемых для имитации равномерно распределенных на [0, 1] случайных величин. В основе метода - математическое понятие сравнения.
Два целых числа a и b сравнимы по модулю m, если они дают одинаковые остатки при делении на m: a = b [mod m]
Обозначим черев γ равномерно распределенную величину на интервале [0, 1]. Пусть x0 и m - целые числа, и x0 взаимно просто с a. Если γ0 = x0/m - несократимая дробь, то все γi будут несократимыми дробями γi = xi/m, где числители xi определяются формулой: xi = a xi-1 [mod m]
Пример: н. у.: m = 7, x0 = 1, a = 3. Генерируем последовательность γi : γ0 = x0/m=1/7;
x1 = a x0 [mod m] = 3·1 [mod 7] = 3, γ1 = 3/7;
x2 = a x1 [mod m] = 3·3 [mod 7] = 2, γ2 = 2/7;
…
x6 = a x5 [mod m] = 3·5 [mod 7] = 1, γ6 = 1/7;
x7 = a x6 [mod m] = 3·1 [mod 7] = 3, γ7 = 3/7;
…
Из примера видно, что, начиная с какого-то
числа, возникает повторение ранее
генерированных чисел. Период приблизительно
определяется значением модуля. Оценка
отрезка апериодичности может быть
произведена по формуле:
![]() ,
где M
[L]
- математическое ожидание отрезка
апериодичности; N
- количество чисел в данном конечном
множестве (может оцениваться модулем
m).
,
где M
[L]
- математическое ожидание отрезка
апериодичности; N
- количество чисел в данном конечном
множестве (может оцениваться модулем
m).
Полученные числа, учитывая их периодичность,
называют псевдослучайными. В одной
задаче можно использовать совокупность
чисел до первого повтора. После
получения псевдослучайных чисел
необходимо произвести с помощью
специальных тестов проверку их
качества (проверка на случайность и
равномерность). Такая проверка носит
статистический характер, и для
проверки «случайности» можно использовать
критерий серий, а для проверки
«равномерности» - известные статистические
критерии согласия (критерий
![]() или критерий Колмогорова). Для визуального
контроля результатов моделирования
можно построить гистограмму и график
эмпирической плотности распределения.
или критерий Колмогорова). Для визуального
контроля результатов моделирования
можно построить гистограмму и график
эмпирической плотности распределения.
Для
построения гистограммы
интервал изменения данных, в данном
случае [0,1], делится на несколько
непересекающихся интервалов равной
ширины. Количество разбиений k
зависит от объема выборки, и может быть
оценено по одной из формул:
![]() или
или
![]() .
Обычно используют нечетное число
разбиений от 5 до 20. Для каждого интервала
подсчитывают частоту попаданий.
Гистограмму можно построить как
столбиковую диаграмму с высотой
столбиков, равной относительной частоте
попаданий в интервал. Многие
популярные программные пакеты имеют
средства для визуализации данных и для
проведения статистического анализа.
.
Обычно используют нечетное число
разбиений от 5 до 20. Для каждого интервала
подсчитывают частоту попаданий.
Гистограмму можно построить как
столбиковую диаграмму с высотой
столбиков, равной относительной частоте
попаданий в интервал. Многие
популярные программные пакеты имеют
средства для визуализации данных и для
проведения статистического анализа.
Для
проверки на «случайность» возможно
использование критерия
серий.
Гипотезы: H0
- последовательность наблюдений
образует случайную выборку. H1
- отрицание нулевой гипотезы. Если
последовательность чисел x1,
x2,…,
xn
носит
случайный характер, то и последовательность
знаков разностей
![]() будет случайной. Серией называется
последовательность одинаковых знаков.
В качестве статистики критерия t
используется количество серий. В качестве
критических границ используются границы
доверительного интервала количества
серий в выборке данного объема
будет случайной. Серией называется
последовательность одинаковых знаков.
В качестве статистики критерия t
используется количество серий. В качестве
критических границ используются границы
доверительного интервала количества
серий в выборке данного объема
![]() ,
где
,
где
![]() ,
,
![]() ,
n(+),
n(-)
> 20,
,
n(+),
n(-)
> 20,
![]() ,
F
– функция стандартного нормального
распределения. Н0
принимается, если количество серий
попадает внутрь интервала.
,
F
– функция стандартного нормального
распределения. Н0
принимается, если количество серий
попадает внутрь интервала.
Для проверки соответствия данных некоторому закону распределения можно использовать критерий χ2. Н0: в основе выборки лежит равномерное распределение с параметрами (0, 1). H1: выборка принадлежит к неизвестному распределению F(x).
В основе лежит сравнение эмпирического распределения выборки, выраженного абсолютными частотами сгруппированного ряда измерений, с гипотетическим теоретическим распределением соответствующей генеральной совокупности.
Различие между эмпирическим и предполагаемым теоретическим распределениями можно характеризовать нормированной суммой квадратов уклонений между hi (наблюдаемыми) и npi (ожидаемыми) частотами — так называемой величиной «хи-квадрат»:
![]()
Соответствующая
данной реализации случайная величина
χ2,
согласно
Пирсону, приближенно удовлетворяет
χ2-распределению
с т=k-1
степенями
свободы. При истинности гипотезы
Н0.
Если вычисленное по выборке значение
![]() ,
то гипотеза согласия принимается.
Ожидаемая частота попадания во внутренние
интервалы не должна быть меньше 5, а для
крайних интервалов – меньше 1.
,
то гипотеза согласия принимается.
Ожидаемая частота попадания во внутренние
интервалы не должна быть меньше 5, а для
крайних интервалов – меньше 1.
