7. Методом Пуанкаре найти приближенно периодические решения дифференциального уравнения
Решение.
Периодическое решение будем искать в виде ряда по степеням малого параметра, то есть в виде
Тогда
(7.1)
Подставим ряды (7.1) в исходное уравнение
Приравняем
коэффициенты при одинаковых степенях
параметра
в левой и правой частях последнего
равенства:
(7.2)
…………………………………..
В (7.2) существует
2 решения:
1) Рассмотрим случай
.
Тогда из второго уравнения системы (7.2):
.
Решение этого уравнения складывается из суммы частного и общего решений. Найдём общее решение:
характеристическое
уравнение будет иметь вид:
.
Тогда
,
но период этого
решения
,
т.е. оно не порождает
-периодических
решений, поэтому решение уравнения
будем искать в виде
.
Продифференцировав 2 раза, получим
Тогда
Будем искать
из третьего уравнения системы (7.2).
Имеем:
,
или
,
.
Решение будет
иметь вид
.
Тогда, подставляя в уравнение, получим:
.
Итак, приближенное периодическое решение имеет вид:
;
Или же:
.
2) Теперь, рассмотрим
случай
.
Тогда из второго уравнения системы (7.2):
.
Решение этого уравнения складывается из суммы частного и общего решений. Найдём общее решение:
характеристическое
уравнение будет иметь вид:
.
Тогда
.
Это решение имеет
период
,
т.е. оно так же не порождает
-периодических
решений, поэтому решение уравнения
будем искать в виде
.
Продифференцировав 2 раза, получим
Тогда
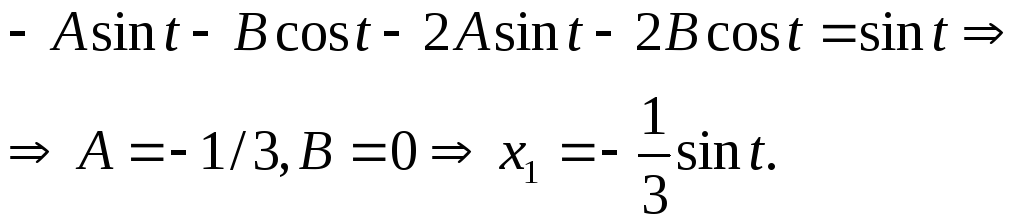
Будем искать
из третьего уравнения системы (7.2).
Имеем:
,
.
Решение будет
иметь вид
,
Тогда, подставляя в уравнение, получим:
.
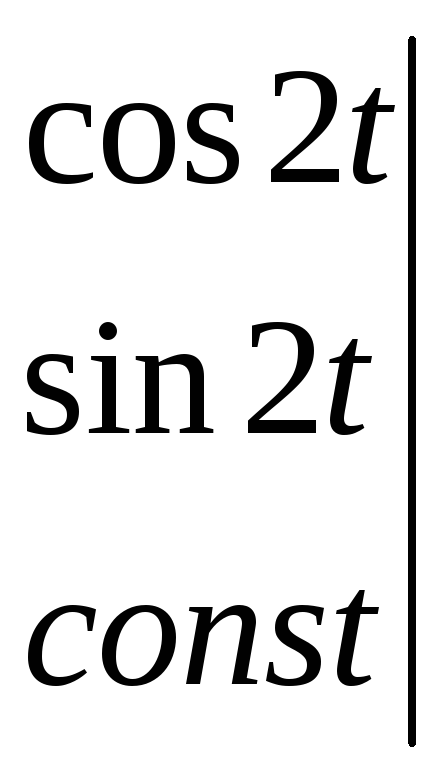
Таким образом, приближенное периодическое решение имеет вид:
.
Или же:
Используя пакет
MathCAD, сравним полученные решения с точным
решением исходного уравнения на периоде
.
Для
:
Для
:
Список литературы:
-
Буркин И.М. Обыкновенные дифференциальные уравнения. Методы интегрирования. Теория устойчивости. Теория колебаний. Тула: ТулГУ, 2004.
-
Федорюк М.В. Обыкновенные дифференциальные уравнения. – 2-е изд., перераб. и доп. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 448 с.
-
Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. - М.: Наука, 1979. - 128 с.
4. Пантелеев А.В., Якимова А.С., Босов А.В.«Обыкновенные дифференциальные уравнения в примерах и задачах». – Москва,2000
5. Тихонов А.Н., Васильева А.Б., Свешников А.Г.«Дифференциальные уравнения». – Москва,2002