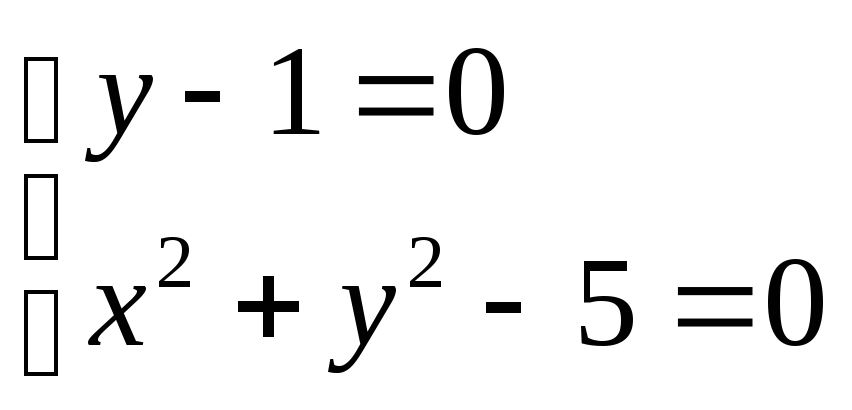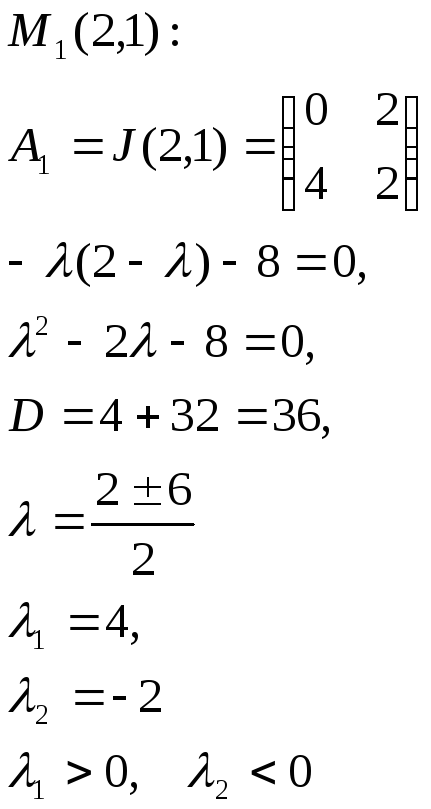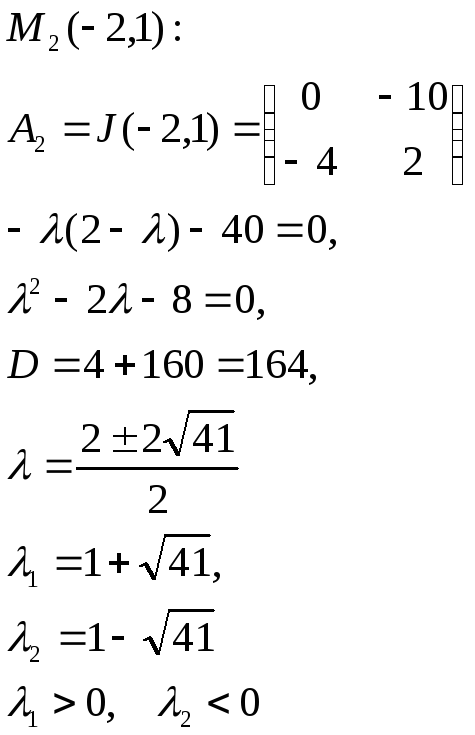Федеральное агентство по образованию РФ
Государственное образовательное учреждение высшего
профессионального образования
Тульский государственный университет
Кафедра математического анализа
Курсовая работа
по курсу “Дифференциальные уравнения”
на тему:
“Элементы качественной теории
Обыкновенных дифференциальных уравнений и теории колебаний”
Автор работы ст. гр. 520191 Ульченков М.А.
подпись дата
Руководитель работы асс. каф. мат.ан. Соболева Д. В.
подпись дата
Работа защищена Оценка __________________
дата
Тула 2011
Содержание
|
|
стр. |
|
Пояснительная записка |
3 |
|
Задание № 1. |
4 |
|
Задание № 2 |
10 |
|
Задание № 3 |
18 |
|
Задание № 4 |
20 |
|
Задание № 5 |
22 |
|
Задание № 6 |
24 |
|
Задание № 7 |
28 |
|
Список литературы |
33 |
Пояснительная записка
В данной курсовой работе рассматриваются основные аспекты качественной теории обыкновенных дифференциальных уравнений на примере решения задач, посвященных нахождению особых точек и исследованию их характера для нелинейной автономной системы 2-го порядка; нахождению первого интеграла и построению фазового портрета нелинейного автономного уравнения 2-го порядка; исследованию устойчивости и асимптотической устойчивости нулевого решения линейного однородного уравнения 4-го порядка с постоянными однородного уравнения 4-го порядка с постоянными коэффициентами; построению функции Ляпунова для нелинейной автономной системы 2-го порядка; исследованию асимптотической устойчивости нулевого решения нелинейной автономной системы 2-го порядка с помощью линеаризации правых частей (первого приближения); исследованию диссипативности нелинейной автономной системы 2-го порядка и существовании у нее циклов; приближенному построению с помощью метода малого параметра периодического решения нелинейного неавтономного уравнения 2-го порядка. Особое внимание уделено построению фазовых траекторий в окрестностях особых точек и фазового портрета.
Объем курсовой работы составляет 33 стр.
1. Найти особые точки системы. Определить их тип. Построить схематически фазовый портрет в окрестностях каждой особой точки.
Решение.
Для нахождения особых точек, необходимо решить систему
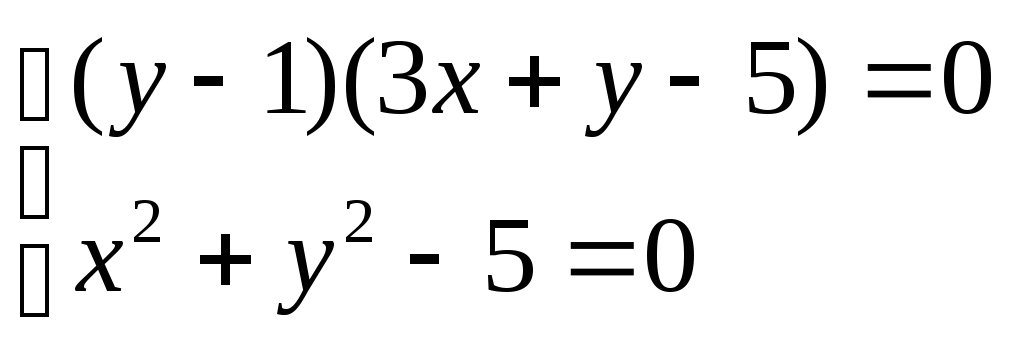
Разобьем ее на две:
|
|
|
Таким образом, мы имеем 4 особые точки:
.
Построим Якобиан системы:
|
Тип точки – седло |
Тип точки - седло |
Тип точки – устойчивый фокус |
|
Тип точки – неустойчивый узел |
||
Рассмотрим точки подробнее:
Рис 1.1 Схематический
портрет особой точки
Рис 1.2 Схематический
портрет особой точки
Для определение
направления закручивания, построим
вектор направления в окрестностях
Рис 1.3 Схематический
портрет особой точки
Рис 1.4 Схематический
портрет особой точки
Проверим полученный результат в пакете Maple:
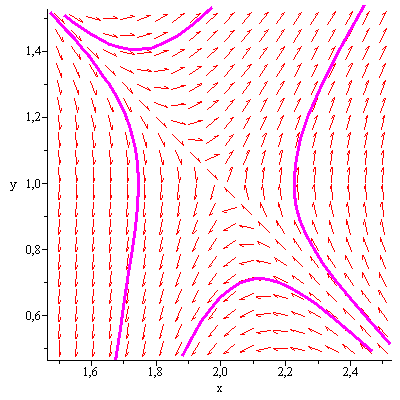
Рис 1.5 Фазовый
портрет особой точки
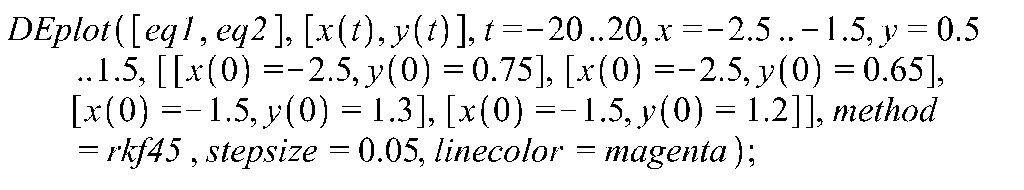
Рис 1.6 Фазовый
портрет особой точки
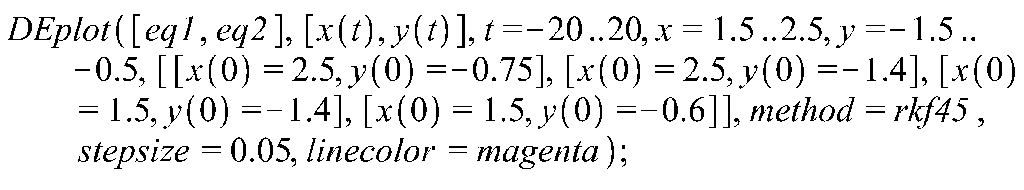
Рис 1.7 Фазовый
портрет особой точки
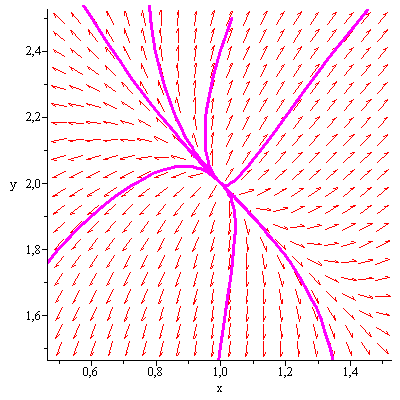
Рис 1.8 Фазовый
портрет особой точки
