
- •10.Траектории, скорости и ускорения точек тела при его поступательном и вращательном движении.
- •2.Скорость и ускорение точки при векторном и координатном способах задания движения.
- •Вектор скорости
- •3.Скорость и ускорение точки при естественном способе задания движения.
- •4.Касательное и нормальное ускорения.
- •5.Равномерное и равнопеременное движения точки.
- •6.Плоское движение твердого тела. Определение скоростей и ускорений точек.
- •7.Теорема о проекциях скоростей двух точек плоской фигуры. Мгновенный центр скоростей.
- •9.Вращательное движение твердого тела вокруг неподвижной оси. Уравнение движения, угловая скорость и угловое ускорение.
3.Скорость и ускорение точки при естественном способе задания движения.
Предельное
положение прямой, проходящей через
точки М
и М1
траектории L
точки М, когда М1
стремится к М, определяет касательную
к этой кривой в точке М. Обозначим
 - единичный направляющий вектор
касательной к L
в точке М.
- единичный направляющий вектор
касательной к L
в точке М.
Соприкасающаяся плоскость в точке М кривой L определяется как предельное положение плоскости, содержащей в себе касательную в точке М кривой и любую точку М1 на ней, когда М1 стремится к М.
Нормаль
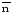 к кривой в точке М, лежащую в соприкасающейся
плоскости, называют главной
нормалью к
кривой в т.М. Нормаль
к кривой в точке М, лежащую в соприкасающейся
плоскости, называют главной
нормалью к
кривой в т.М. Нормаль
 к кривой, перпендикулярную соприкасающейся
плоскости, называют бинормалью.
к кривой, перпендикулярную соприкасающейся
плоскости, называют бинормалью.
Прямоугольную
систему взаимно ортогональных осей,
направленных по
 называют естественными
осями кривой L.
называют естественными
осями кривой L.
Направление
вектора скорости принимают за
положительное направление касательной
 .
Положительное направление главной
нормали считают в сторону вогнутости
кривой, а бинормаль направляют так,
чтобы получившаяся система осей
.
Положительное направление главной
нормали считают в сторону вогнутости
кривой, а бинормаль направляют так,
чтобы получившаяся система осей
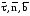 являлась правой.
являлась правой.
Кривизной «k» кривой L в точке М называют предел
 .
.
Радиусом кривизны «» кривой L в точке М называют величину обратную ее кривизне в этой точке
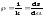 .
.
Так,
например, дуга окружности длиной s,
опирающаяся на центральный угол
 ,
,
 ,
где R
– радиус окружности, то радиус
кривизны
для окружности
,
где R
– радиус окружности, то радиус
кривизны
для окружности 
 .
.
4.Касательное и нормальное ускорения.
Ускорение
точки можно разложить на тангенциальное
 ,
направленное по касательной к траектории
и характеризующее изменение величины
скорости, и
,
направленное по касательной к траектории
и характеризующее изменение величины
скорости, и 
нормальное
 ,
направленное по главной нормали к
центру кривизны С траектории и
определяющее изменение направления
,
направленное по главной нормали к
центру кривизны С траектории и
определяющее изменение направления
 .
.
Так
как в естественных осях траектории
скорость может быть представлена в
виде
 ,
то, дифференцируя это соотношение по
времени, получим ускорение
,
то, дифференцируя это соотношение по
времени, получим ускорение
 ,
Касательное ускорение
(проекция ускорения точки на касательную)
равно первой производной от величины
скорости от времени.
,
Касательное ускорение
(проекция ускорения точки на касательную)
равно первой производной от величины
скорости от времени.
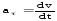
Нормальное ускорение

Абсолютная
величина
 может быть определена по формуле
может быть определена по формуле
 .
.
5.Равномерное и равнопеременное движения точки.
точки
- движение, при к-ром касат. ускорение
w
т
точки (в случае прямолинейного движения
полное ускорение w
)постоянно. Закон Р. д. точки и закон
изменения её скорости u
при этом движении даются равенствами:
![]()
где
s - измеренное вдоль дуги траектории
расстояние точки от выбранного на
траектории начала отсчёта, t-
время, s0
- значение s в нач. момент времени t = = 0.
![]() -
нач. скорость точки. Когда знаки u
и w
одинаковы, Р. д. является ускоренным, а
когда разные - замедленным.
-
нач. скорость точки. Когда знаки u
и w
одинаковы, Р. д. является ускоренным, а
когда разные - замедленным.
При поступат. Р. д. твёрдого тела всё сказанное относится к каждой точке тела; при равномерном вращении вокруг неподвижной оси угл. ускорение e тела постоянно, а закон вращения и закон изменения угл. скорости w тела даются равенствами
![]()
где f - угол поворота тела, f0 - значение f в нач. момент времени t = 0, w0 - нач. угл. скорость тела. Когда знаки w и e совпадают, вращение является ускоренным, а когда не совпадают - замедленным.
Равномерное движение-движение точки, при котором численная величина ее скорости постоянна.
