Кинематика.

1.Способы задания движения точки. Траектория движения. Движение тела или материальной точки считают известным, если существует возможность определить их положение относительно выбранной системы отсчета в любой момент времени. Задание движения точки может быть осуществлено естественным или координатным способами. Геометрическое место всех положений движущейся точки М называют её траекторией.

8.Сложение скоростей при сложном движении точки. Сложение скоростей.

Рассмотрим точку М, совершающую сложное движение. Пусть эта точка, двигаясь вдоль своей относительной траектории АВ, совершает за промежуток времени относительное перемещение, определяемое вектором ММ (рис. .

Теорема о сложении скоростей: при сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей.

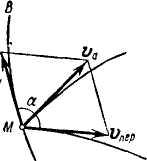
Если угол между направлениями векторов v_отн и v_neр равен α, то по модулю:

v_а²=v_отн²+v_neр²+2 v_отнv_neрcosα

10.Траектории, скорости и ускорения точек тела при его поступательном и вращательном движении.

При поступательном движении любой отрезок прямой (например, отрезок АВ), проведенный в твердом теле, остается параллельным самому себе.

Выберем подвижную систему отсчета Axyz , оси которой связаны с данным телом и передвигаются вместе с ним.

Т. к. при поступательном движении оси координат остаются параллельными своему начальному направлению, координаты любой точки (например т. В) твердого тела в подвижной системе отсчета остаются постоянными, а ее движение тождественно движению т. А.

Следовательно, траектории движения всех точек одинаковы. Одинаковыми по модулю и направлению будут также скорости и ускорения твердого тела при его поступательном движении.

Поступательное движение твердого тела полностью определяется движением одной его точки.

Все точки тела движутся по идентичным траекториям, а их скорости и ускорения одинаковы.

Скорости и ускорения при простейших движениях точек тела при его поступательном движении

1. Равномерное прямолинейное движение (v=const) по оси Х

x=x₀+vt, a=0.

2. Равномерное криволинейное движение (v=const)

s=s₀+vt,

где s − дуговая координата; s₀ − дуговая координата в начальный момент времени при t=0.

3. Равноускоренное движение (a=const)

v=v₀+ а_τ t

,здесь v₀ − начальная скорость при t=0.

2.Скорость и ускорение точки при векторном и координатном способах задания движения.

Векторный способ задания движения: Положение точки М в пространстве определяется её радиус–вектором 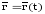. Траекторией является геометрическое место концов вектора

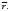
Вектор скорости

Скоростью точки М, определяющей как быстро и в каком направлении она движется в данный момент времени t, называют предел

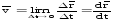
Вектор скорости равен первой производной от радиуса-вектора точки по времени.

Так как предельным положением секущей ММ₁ является касательная к траектории точки, то и вектор ее скорости 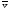в данный момент времени t направлен по касательной к траектории в сторону движения. Вектор ускорения

Величину 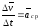называют средним ускорением точки за время 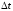. Предел отношения

,

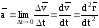характеризующий изменение скорости в данный момент времени t, называют ускорением точки.

Вектор ускорения равен первой производной от вектора скорости точки по времени или второй производной от радиуса-вектора точки по времени.

Ускорение 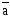, направлено в сторону вогнутости траектории.

Координатный способ задания движения. В прямолинейной системе координат Oxyz вектор 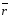может быть представлен в виде

,

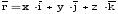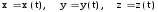
• координаты точки М, определяющие закон ее движения в зависимости от времени t ;

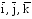• - нормированный базис Oxyz.

Согласно теореме о проекциях производной вектора.

1. Проекции скорости на оси координат равны первым производным от соответствующих координат точки по времени:

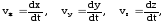
2. Проекции ускорения на оси координат равны первым производным от проекций скоростей точки или вторым производным от соответствующих координат точки по времени:

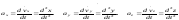
Величины (модули) скорости и ускорения в декартовой ортогональной системе координат определяют по формулам

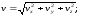
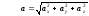
а направления 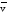и 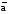характеризуют их направляющие косинусы

.