Л 15, 16, 17, 18 .

3.2. Характеристики линейных активных четырехполюсников.

Активной называют цепь, коэффициент передачи мощности которой больше единицы. С точки зрения закона сохранения энергии такое возможно, если в цепи действует дополнительный источник энергии, энергия которого преобразуется в энергию выходного сигнала. Преобразование осуществляется с помощью транзисторов, электронных ламп и других элементов, называемых активными. Эквивалентное представление цепи определяется режимом работы активного элемента. Для малых амплитуд переменного сигнала характеристики активных элементов практически линейны. В этом случае активную цепь можно представить линейным четырехполюсником. Анализ показывает, что большинство активных четырехполюсников невзаимны, то есть Z₁₂Z₂₁. (см. § 3.1).

На входе активных четырехполюсников действуют источники управляющих (входных) сигналов, а к выходу подключено сопротивление нагрузки . Под выходным напряжением при этом подразумевается падение напряжения на сопротивлении нагрузки.

Все основные свойства активных линейных цепей, т.е основные параметры передаточной характеристики, эффекты обратной связи, критерии устойчивости цепей с обратной связью - будем рассматривать на основе ранее изложенной теории линейного четырехполюсника.

Для вывода соотношений, описывающих основные характеристики линейных активных цепей, запишем матрицу вида (3) в виде системы уравнений :

(17)

С точки зрения электроники для двухконтурной системы соотношение (17) является системой уравнений, составленной на основании Законов Кирхгофа по методу контурных токов, в качестве которых выступают входной и выходной токи, заданные своими комплексными амплитудами. На рисунке изображена эквивалентная схема четырехполюсника, построенная в соответствии с уравнениями (17). В этой схеме с помощью источника ЭДС учтено влияние напряжения на выходных зажимах четырехполюсника на величину , а с помощью источника тока - влияние входного тока на ток .

.

J₁

.

J₂

.

J_н

h₁₁

.

h₁₂U₂

R_г

.

U₁=U_г-I₁R_г

U_н

.

Z_н

_-1

h₂₂

~

.

h₂₁J₁

.

U₂

Поскольку I₂=-I_н , и второе уравнение (17) примет вид . Отсюда для частотного коэффициента передачи по току находим:

(18)

где .

Частотный коэффициент передачи по напряжению найдем исключив ток из первого уравнения (17), и использовав для этого (18) :

(19)

где h’=h₁₁h’₂₂‑h_12­h₂₁.

Для активного четырехполюсника коэффициенты передачи (18) и (19) называют коэффициентами усиления по току и напряжению.

Входное сопротивление активного четырехполюсника найдем из первого уравнения (17) опять используя формулу (18)

(20)

Выходное сопротивление Z_BbIX - сопротивление на разомкнутых выходных зажимах четырехполюсника при подключенном по входу источнике сигала с внутренним сопротивлением R_Г (т.е. полагая, что ) - найдем из второго уравнения (17)

При U_Г=0, это означает независимость параметров четырехполюсника от входного напряжения , где . Окончательно для получаем

(21)

Полученные соотношения заметно упрощаются при условии :

(22)

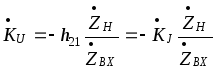
Проанализируем физический смысл h-параметры активного четырехполюсника. Для этого представим первое уравнение системы (17) в виде функциональной зависимости . Используя разложение этой зависимости в ряд Тейлора по малым приращениям входного тока  и выходного напряжения , найдем приращение входного напряжения , в виде

Сравнив полученное соотношение с первым уравнением (17), получаем , (23)

Малыми приращениями являются малые переменные токи и напряжения. Таким образом, для малых сигналов параметры h₁₁, h₁₂ и очевидно, h₂₂ и h₂₁ являются дифференциальными и представляют собой наклон характеристик U₁(J₁) и U₁(U₂) в окрестности заданной рабочей точки. Эти характеристики для активных элементов не являются линейными, поэтому система уравнений справедлива, строго говоря, при исчезающе малой амплитуде входных воздействий. Тем не менее положение рабочей точки может быть выбрано таким образом, что, в довольно широкой области вблизи нее, характеристики могут считаться линейными с достаточной степенью точности. На практике считают, что понятие h-параметров относятся к переменным малым напряжениям и токам.

Самостоятельно

1. Вывести соотношения вида (23) для h₂₂ и h₂₁.

2. Получить соотношения вида (22) и (23) для систем Z- и y-параметров.