54 . Ошибки 1 и 2 рода

Статистическое решение может быть ошибочным. При этом различают ошибки I-го и II-го родов.Опр. Ошибкой первого рода называется ошибка, состоящая в том, что гипотеза Н₀ отклоняется, когда Н₀ – верна. Вероятность P{ZV_kH₀}=..ОпрОшибкой второго рода называется ошибка, состоящая в том, что принимается гипотеза Н₀, но в действительности верна альтернативная гипотеза Н₁. Вероятность ошибки второго рода при условии, что гипотеза Н₁ – простая, P{ZV\V_kH₁}=.Проверка статистических гипотез и доверительных интервалов.Проверка гипотез с использованием критерия значимости может быть проведена на основе доверительных интервалов. При этом одностороннему критерию значимости будет соответствовать односторонний доверительный интервал, а двустороннему критерию значимости будет соответствовать, двусторонний доверительный интервал. Гипотеза Н₀ – принимается, если значение ₀ накрывается доверительным интервалом, иначе отклоняется.

55. Критерий и его применение.

Критерий применяется в частности для проверки гипотез о виде распределения генеральной совокупности.

Процедура применения критерия для проверки гипотезы H₀, утверждающей, что СВ Х имеет закон распределения состоит из следующих этапов.

Этапы:

1. По выборке найти оценки неизвестных параметров предполагаемого закона .

2. Если Х–СВДТ – определить частоты , i = 1, 2, …, r, с которым каждое значение встречается в выборке.

Если Х–СВНТ – разбить множество значений на r – непересекающихся интервалов и попавших в каждый из этих интервалов .

3. Х–СВДТ вычислить .

Х–СВНТ вычислить .

4. .

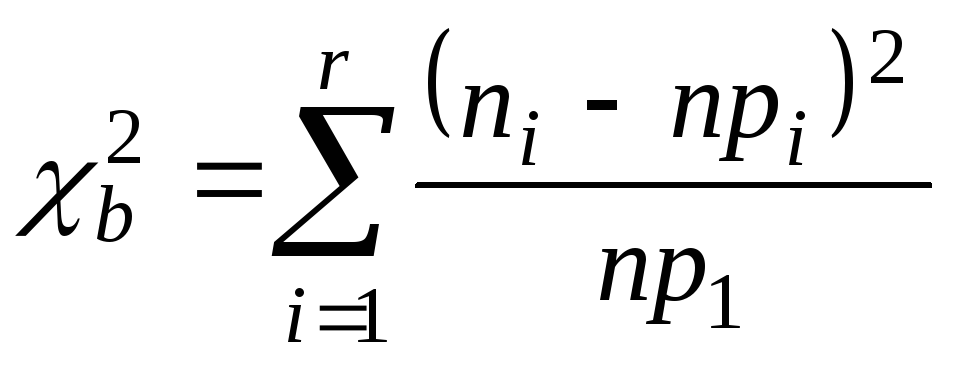5. Принять статистическое решение.

– гипотеза Н₀ – принимается.

– гипотеза Н₀ – отклоняется.

e – количество оцениваемых параметров.

Малочисленные частоты надо будет объединять.

Проверка гипотезы о равномерном распределении генеральной совокупности.

n = 200

А;

№	(xi-1, xi)	ni
1	2 – 4	21	 =0,05
2	4 – 6	16
3	6 – 8	15
4	8 – 10	26
5	10 – 12	22
6	12 – 14	14
7	14 – 16	21
8	16 – 18	22
9	18 – 20	18
10	20 – 22	25

1.

2.

21	17,3	0,79
16	20	0,8

k = 10 – 2 – 1 = 7

– нет основания отвергать гипотезу о том, что выборка взята из генеральной совокупности и имеет равномерное распределение.